Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N , состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.
Сформулируем следующие определения:
Размещения без повторения
Размещением без повторения из n элементов по m N , содержащее m различных элементов .
Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.
Теорема 3 . Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n . Записывают:
Перестановки без повторений
Перестановками из n элементов называются различные упорядочения множества N .
Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.
Теорема 4 . Число различных перестановок без повторений вычисляется по формуле
Сочетания без повторений
Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N , содержащее m различных элементов.
Из определения следует, что два сочетания различаются только элементами, порядок не важен.
Теорема 5 . Число сочетаний без повторений вычисляют по одной из следующих формул:
Пример 1 . В комнате 5 стульев. Сколькими способами можно разместить на них
а) 7 человек; б) 5 человек; в) 3 человека?
Решение:
а) Прежде всего надо выбрать 5 человек
из 7 для посадки на стулья. Это можно
сделать
способом. С каждым выбором конкретной
пятерки можно произвести
перестановок местами. Согласно теореме
умножения искомое число способов посадки
равно.
Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно . Решения обоими способами согласуются, так как
б) Решение очевидно
-
в)
- число выборов занимаемых стульев.
- число размещений
трех человек на трех выбранных стульях.
Общее число выборов равно .
Не трудно проверить
формулы
;
;
Число всех подмножеств множества, состоящего из n элементов.
Размещения с повторением
Размещением с повторением из n элементов по m называется всякое упорядоченное подмножество множества N , состоящее из m элементов так, что любой элемент ожжет входить в это подмножество от 1 до m раз, либо вообще в нем отсутствовать .
Число
размещений с повторением обозначают
и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
Пример 2
.
Пусть дано множество из трех букв N
= {a,
b,
c}.
Назовем словом любой набор из букв,
входящих в это множество. Найдем
количество слов длиной 2, которые можно
составить из этих букв:
.
Замечание:
Очевидно, размещения с повторением
можно рассматривать и при
.
Пример 3 . Требуется из букв {a, b}, составить всевозможные слова длиной 3. Сколькими способами это можно сделать?
Ответ
:
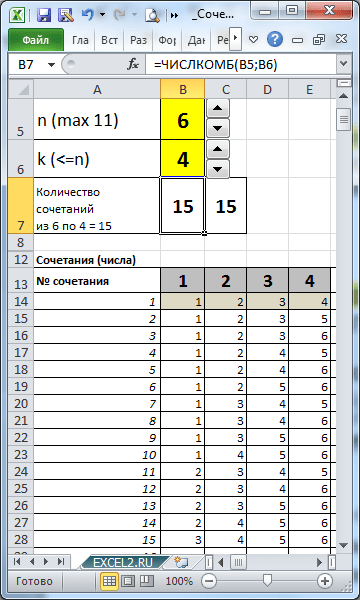
Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).
Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примечание : Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье - плохая идея.
Отличие Сочетаний от Размещений
Вывод всех комбинаций Сочетаний
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.
Задача
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.
Нам нужно определить число Сочетаний 7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
НЕУПОРЯДОЧЕННЫЕ УПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ С ФИКСИРОВАННЫМИ РАЗМЕРАМИ ЧАСТЕЙ
Цель: Изучить на практике методику расчета числа перестановок без повторений и с повторениями
Задание 4 () .
Задание 5 (начисло перестановок с повторениями).
Задание 6 (начисло неупорядоченных разбиений с фиксированными размерами частей) .
Задание 7 () .
Задание 4 (начисло перестановок без повторений) .
Сколько различных n n штук цифр: 1,3,5,7,9?
ЧИСЛО ПЕРЕСТАНОВОК БЕЗ ПОВТОРЕНИЙ. КРАТКАЯ ТЕОРИЯ
Перестановками без повторений или просто перестановками из элементов п различных типов называются их последовательности, отличающиеся друг от друга только порядком входящих в них элементов. (Здесь и дальше под последовательностью из п элементов понимается их линейно упорядоченное множество, аналогичное п книгам, стоящим в ряд на полке.)
Пример. Перестановки из 3 различных элементов а, b и с: аbс, bса, саb, сbа, bас, асb.
Число всех перестановок из п различных элементов (обозначается Р п) есть Р п = 1 2 3 ... n = п ! (п ! читается "эн-факториал").
В таблице ниже приведены числовые значения факториалов первых натуральных чисел и нуля.
Таблица. Значения факториалов первых натуральных чисел и нуля.
| n= | |||||||||||
| n!= |
КОНЕЦ ТЕОРИИ.
Решение.
В задании 4 n =5, ибо переставляются местами всевозможными способами n =5 штук различных цифр: 1,3,5,7,9. При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок без повторений из n =5 штук различных элементов.
Согласно теории, искомое число равно Р 5 = 5!= 120 различных 5– значных телефонных номеров.
Ответ: 120 различных 5– значных телефонных номеров.
Задание 5 (на число перестановок с повторениями.)
Сколько различных n – значных телефонных номеров (натуральных чисел) можно написать, переставляя следующий набор n штук цифр: 1,1,1,3,3,5?
ЧИСЛО ПЕРЕСТАНОВОК С ПОВТОРЕНИЯМИ. КРАТКАЯ ТЕОРИЯ
Перестановки с повторениями
Перестановками с повторениями из т элементов n различных типов, среди которых k 1 одинаковых элементов 1-го типа, k 2 одинаковых элементов 2-го типа, ... , k n одинаковых элементов п -го типа (k 1 + k 2 + ... + k п = m ) , называются их последовательности, отличающиеся только порядком входящих в них элементов.
Пример. Перестановки из 3 элементов, среди которых 2 одинаковых элемента типа а и 1 элемент типа b: ааb, аbа, bаа.
Число перестановок из т элементов, среди которых k 1 - одинаковых элементов 1-го типа, k 2 одинаковых элементов2-го типа,..., k п - одинаковых элементов n -го типа [обозначается Р (m ; k 1 ,k 2 ,..., k п) ] равно:
Р (m ; k 1 ,k 2 ,..., k п) = т!/ (k 1 !k 2 !... k п !).
Для примера перестановок с повторениями из 3 элементов, среди которых 2 одинаковых типа а и 1 элемент типа b, имеем Р (m=3 ; k 1 =2,k 2 =1) = 3!/ (2 !1!).
КОНЕЦ ТЕОРИИ.
Решение.
В задание 5 m =6, ибо переставляются местами всевозможными способами m =6 штук различных цифр: 1,1,1,3,3,5, среди которых есть повторяющиеся (одинаковые). При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок с повторениями из m =6 штук элементов, среди которых k 1 =3 одинаковых элементов 1-го типа (цифра 1), k 2 =2 одинаковых элементов2-го типа (цифра 3), k 3 =1одинаковых элементов 3 -го типа (цифра 5), равно Р (m ; k 1 ,k 2 ,..., k п) = т!/ (k 1 !k 2 !... k п !), Р (6; 3, 2, 1) = 6!/(3! 2! 1!)= =60.
Ответ: Р (6; 3, 2, 1) = 60, т. е 60 различных вариантов 6– значных телефонных номеров (6-значных чисел), содержащих цифру 1 трижды, 3 -дважды и 5 - один раз.
Задание 6 (на число неупорядоченных разбиений с фиксированными размерами частей) .
Сколько всего вариантов можно получить, разбивая группу из пяти человек (из пяти солдат) на три подгруппы - две подгруппы по два человека (по два автоматчики) и одна подгруппа из одного человека (из одного пулеметчика)?
НЕУПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ. КРАТКАЯ ТЕОРИЯ
Неупорядоченное разбиение n -элементного множества X - это любое семейство {X 1 , X 2 ,…, X k }, где 1≤k≤п; X 1 , X 2 ,…, X k - непустые попарно непересекающиеся подмножества множества X , объединение которых равноX.
Называем такое разбиение неупорядоченным, так как семейство - это неупорядоченная совокупность.
Пример. Для множества {а,b,с} неупорядоченное разбиение это, например, {{а},{b,с}}. Причем {{а},{b,с}}={{b,с},{а}}.
Для множества с п элементами обозначим через D (n ; k 1 , k 2 ,…, k n) число всех таких неупорядоченных разбиений, в которых есть k 1 подмножеств с одним элементом, k 2 подмножеств с двумя элементами и т.д., где k 1 ≥0, k 2 ≥0,…, k n ≥0; k 1 +2 k 2 +…+n k n = n.
КОНЕЦ ТЕОРИИ.
Решение.
Каждый вариант- это неупорядоченное разбиение { Иванов, Петров, Сидоров, Андреев, Борисов }. Множество из 5 элементов Один из вариантов разбиения {{Иванов, Петров}, {Сидоров, Андреев}, {Борисов}}
Имеем п = 5, k 1 =1, k 2 =2, k 3 =0, k 4 =0, k 5 =0 (так как по условию нет подгрупп из трех, четырех, пяти человек).
Ответ: 15 вариантов.
Задание 7 (начисло упорядоченных разбиений с фиксированными размерами частей) .
Сколькими способами можно выбрать из десяти солдат трех пулеметчиков, трех гранатометчиков и четырех автоматчиков (3 пулеметчика 3 гранатометчика 4 автоматчика, всего 10 солдат)?
УПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ. КРАТКАЯ ТЕОРИЯ
Упорядоченным разбиением конечного множества X с n элементами называется любой кортеж вида <X 1 , X 2 ,…, X k >, где 1 ≤k ≤n ; X 1 , X 2 ,…, X k - непустые попарно непересекающиеся, подмножества множества X, объединение которых равно X.
Называем такое разбиение упорядоченным , так как элементы кортежа упорядочены.
Пример. Для множества {а,b,с} упорядоченное разбиение это, например, кортеж <{{а},{b,с}} >. Причем <{{а},{b,с}}> ¹<{{b,с},{а}} >.
Для множества с п элементами обозначим через E (n ; m 1 , m 2 ,…, m k ,) число всех таких упорядоченных разбиений на подмножества X 1 , X 2 ,…, X k , содержащие m 1 , m 2 ,…, m k , где m 1 ≥0, m 2 ≥0,…, m k ≥0; m 1 + m 2 +…+ m k = n.
Число всех
упорядоченных разбиений
<X
1 , X
2 ,…, X
k > множества с п
элементами на подмножества X
1 , X
2 ,…, X
k , содержащие m
1 , m
2 ,…, m
k , элементов соответственно. определяется по полиномиальной формуле
где m 1 ≥1, m 2 ≥1,…, m n ≥1; m 1 + m 2 +…+m k = n.
КОНЕЦ ТЕОРИИ.
Решение.
В задании имеем упорядоченное разбиение < X 1 , X 2 , X 3 > множества с десятью элементами, где X 1 - подмножество пулеметчиков, Х 2 - подмножество гранатометчиков, Х 3 - подмножество автоматчиков;
поэтому п = 10, m 1 = 3, т 2 , = 3, т 3 = 4.
Тогда всего есть
Ответ: 4200 вариантов
Рассмотрим сначала некоторые общие термины.
- Пусть некоторая совокупность содержит n элементов, из которых выбирают k элементов. Каждый такой набор будем называть выборкой объема k из n элементов .
- Будем различать выборки с возвращением и без возвращения
. Пусть имеется совокупность n
пронумерованных элементов:
- если отобранный элемент после выбора не возвращается в исходную совокупность и не может повторяться в данной выборке больше одного раза, то такая выборка называется выборкой без возвращения или без повторения ;
- если отобранный элемент после фиксации номера снова возвращается в исходную совокупность и, таким образом, может вновь оказаться в данной выборке, то говорят о выборке с возвращением или с повторением .
- Выборка называется упорядоченной, если порядок следования элементов в ней задан. Если две упорядоченные выборки отличаются только порядком следования элементов, то они считаются разными (например: 12 и 21).
- Выборка называется неупорядоченной, если порядок элементов в ней не имеет значения (т. е. 12 и 21 неразличимы).
Размещения без повторений.
Размещениями без повторений называются упорядоченные выборки, содержащие k различных элементов из данных n элементов.
Обратим внимание на следующие важные положения:
- Порядок элементов в выборке важен.
Формула для определения числа размещений без повторений:
Задача. Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности?
Решение.
По условию код состоит «из двух разных символов», при этом коды АБ и БА – не одинаковые, поэтому, выборки – размещения без повторений.
Выборка осуществляется из 3 элементов по 2. Значит, n = 3, k = 2
.
Действительно, комбинаций, удовлетворяющих условию, всего шесть: {АБ, АС, БА, БС, СА, СБ}
Перестановки без повторений.
Нетрудно заметить, что размещения, в которые входят все n разных элементов заданного множества (т. е. k = n ), будут отличаться только порядком следования входящих элементов. Такие размещения называют перестановками.
Перестановками без повторений называются всевозможные упорядоченные выборки, составленные из всех данных n элементов.
Формула для определения числа перестановок без повторений
P n = n! = n * (n − 1) * (n − 2) *...* 2 * 1
Задача. Сколько вариантов кода длиной 3 символа можно составить из трех букв А, Б, С, если каждая буква входит в последовательность не более одного раза?
Решение.
Так как «каждая буква входит в последовательность не более одного раза», то выборки – перестановки без повторений.
P n = 3! = 3 * 2 * 1 = 6 {АБC, АCБ, БАС, БСА, САБ, СБА}
Сочетания без повторений.
Сочетаниями без повторений называются неупорядоченные выборки, содержащие k различных элементов из данных n элементов.
Отметим, что
- …«выборки неупорядоченные», т.е. выборки AB и ВА – это одно и тоже сочетание.
- Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.
Формула для определения числа сочетаний без повторений:
Задача. Из 4-х кандидатов происходят выборы участников конференции. Сколько существует вариантов выбора делегации?
Решение. Очевидно, один и тот же кандидат в данную выборку может быть избран только один раз. При этом набор А, Б и Б, А – это одни те же участники. Поэтому выборки есть сочетания без повторений.
Воспользуемся формулой для расчета числа различных сочетаний без повторений:
Число размещений без повторений из n по k n k различными координатами.
Число размещений без повторений находится по формуле:
Пример: Сколькими способами можно построить 3-значное число с различными цифрами, не содержащее цифры 0?
Количество цифр
,
размерность вектора с различными
координатами
Число размещений с повторениями
Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.
Число размещений с повторениями находится по формуле:
.
Пример: Сколько слов длины 6 можно составить из 26 букв латинского алфавита?
Количество букв
,
размерность вектора
Число перестановок без повторений
Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.
Число перестановок без повторений находится по формуле:
.
Замечание:
Мощность искомого множества А
удобно искать по формуле:
,
гдех
– число способов выбрать нужные места;
у
– число
способов расположить на них нужные
элементы; z
– число
способов расположить остальные элементы
на оставшихся местах.
Пример. Сколькими способами можно расставить на книжной полке 5 различных книг? В скольких случаях две определенные книги А и В окажутся рядом?
Всего способов
расставить 5 книг на 5-ти местах – равно
= 5! = 120.
В задаче х
– число способов выбрать два места
рядом, х
= 4;
у
– число
способов расположить две книги на двух
местах, у
= 2! = 2;
z
– число
способов расположить остальные 3 книги
на оставшихся 3-х местах, z
= 3! = 6.
Значит
=
48.
Число сочетаний без повторений
Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка.
Число сочетаний без повторений находится по формуле:
.
Свойства:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
Пример. В урне 7 шаров. Из них 3 белых. Наугад выбирают 3 шара. Сколькими способами это можно сделать? В скольких случаях среди них будет ровно один белый.
Всего способов
.
Чтобы получить число способов выбрать
1 белый шар (из 3-х белых) и 2 черных шара
(из 4-х черных), надо перемножить
и
Таким образом искомое количество
способов
Упражнения
1. Из 35 учащихся класс по итогам года имели “5” по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек. Сколько человек имеют “5” по указанным предметам? Сколько человек не имеет “5” по указанным предметам? Имеет “5” только по математике? Имеет “5” только по двум предметам?
2. В группе из 30 студентов каждый знает, по крайней мере, один иностранный язык – английский или немецкий. Английский знают 22 студента, немецкий – 17. Сколько студентов знают оба языка? Сколько студентов знают немецкий язык, но не знают английский?
3. В 20 комнатах общежития института Дружбы Народов живут студенты из России; в 15 – из Африки; в 20 – из стран Южной Америки. Причем в 7 – живут россияне и африканцы, в 8 – россияне и южноамериканцы; в 9 – африканцы и южноамериканцы; в 3 – и россияне, и южноамериканцы, и африканцы. В скольких комнатах живут студенты: 1) только с одного континента; 2) только с двух континентов; 3) только африканцы.
4. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике и астрономии. Три спецкурса посещают 10 студентов, по математике и физике – 30 студентов, по математике и астрономии – 25; спецкурс только по физике – 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике – 145, по астрономии – 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?
5. Староста курса представил следующий отчет по физкультурной работе. Всего – 45 студентов. Футбольная секция – 25 человек, баскетбольная секция – 30 человек, шахматная секция – 28 человек. При этом, 16 человек одновременно посещают футбольную и баскетбольную секции, 18 – футбольную и шахматную, 17 – баскетбольную и шахматную, 15 человек посещают все три секции. Объясните, почему отчет не был принят.
6. В аквариуме 11 рыбок. Из них 4 красных, остальные золотые. Наугад выбирают 4 рыбки. Сколькими способами это можно сделать? Найти число способов сделать это так, чтобы среди них будет: 1) ровно одна красная; 2) ровно 2 золотых; 3) хотя бы одна красная.
7. В списке 8 фамилий. Из них 4 – женские. Сколькими способами их можно разделить на две равные группы так, чтоб в каждой была женская фамилия?
8. Из колоды в 36 карт выбирают 4 . Сколько способов сделать это так, чтобы: 1) все карты были разных мастей; 2) все карты были одной масти; 3) 2 красные и 2 черные.
9. На карточках разрезной азбуки даны буквы К, К, К, У, У, А, Е, Р. Сколько способов сложить их в ряд так, что бы получилось «кукареку».
10. Даны карточки разрезанной азбуки с буквами О, Т, О, Л, О, Р, И, Н, Г, О, Л, О, Г. Сколько способов сложить их так, что бы получилось слово «отолоринголог».
11. Даны карточки нарезной азбуки с буквами Л, И, Т, Е, Р, А, Т, У, Р, А. Сколько способов сложить их в ряд так, что бы получилось слово «литература».
12. 8 человек становятся в очередь. Сколько способов сделать это так, что бы два определенных человека А и Б оказались: 1) рядом; 2) на краях очереди;
13. 10 человек садятся за круглый стол на 10 мест. Сколькими способами это можно сделать так, чтоб рядом оказались: 1) два определенных человека А и Б; 2) три определенных человека А, Б и С.
14. Из 10 арабских цифр составляют 5-значный код. Сколькими способами это можно сделать так, чтобы: 1) все цифры были разными; 2) на последнем месте четная цифра.
15. Из 26 букв латинского алфавита (среди них 6 гласных) составляется шестибуквенное слово. Сколькими способами это можно сделать так, чтобы в слове были: 1) ровно одна буква «а»; 2) ровно одна гласная буква; ровно две буквы «а»; в) ровно две гласные.
16. Сколько четырехзначных чисел делятся на 5?
17. Сколько четырехзначных чисел с различными цифрами делятся на 25?
19. Брошены 3 игральные кости. В скольких случаях выпала: 1) ровно 1 «шестерка»; 2) хотя бы одна «шестерка».
20. Брошены 3 игральные кости. В скольких случаях будет: 1) все разные; 2) ровно два одинаковых числа очков.
21. Сколько слов с различными буквами можно составить из алфавита а, в, с, d. Перечислить их все в лексикографическом порядке: abcd, abcd….
