Sinopsis na temu inverzne funkcije. Međusobno inverzne funkcije. Objašnjenje novog materijala

Bilješke o lekcijama na temu "Inverzne funkcije"

Lekcija 1 "Reverzna funkcija"

Cilj: Formirati teoretsku aparaturu na temu. Enter

Koncept inverzibilne funkcije;

Koncept inverzne funkcije;

Formulirajte i dokažite dovoljan uslov za reverzibilnost

funkcije;

Osnovna svojstva međusobno inverznih funkcija.

Plan predavanja

Organiziranje vremena.

Aktuelizacija znanja učenika, neophodna za sagledavanje nove teme.

Prezentacija novog materijala.

Sumiranje lekcije.

Tok časa-predavanja

1. Organiziranje vremena.

2. Ažuriranje znanja. ( Frontalna anketa na temu prethodne lekcije.)

Za studente na interaktivna tabla prikazan je graf funkcije (slika 1). Nastavnik formuliše zadatak - razmotriti graf funkcije i navesti proučavana svojstva funkcije. Studenti navode svojstva funkcije prema projektu istraživanja. Nastavnik, desno od grafikona funkcije, zapisuje imenovana svojstva markerom na interaktivnoj tabli.

Rice. 1

Svojstva funkcije:

3. Postavljanje ciljeva za učenike.

Na kraju učenja, nastavnik izvještava da će se danas na času upoznati sa još jednim svojstvom funkcije - reverzibilnošću. Za sadržajno proučavanje novog gradiva, nastavnik poziva djecu da se upoznaju sa glavnim pitanjima na koja učenici moraju odgovoriti na kraju časa. Pitanja u formularu handout svaki učenik ima (podijeljeno prije časa).

pitanja:

1. Koja se funkcija naziva reverzibilnom?

2. Koja funkcija se zove inverzna?

3. Kako su povezani domeni definicije i skupovi vrijednosti direktnih i inverznih funkcija?

4. Formulirajte dovoljan uvjet da funkcija bude invertibilna.

5. Da li se inverzna funkcija rastuće funkcije smanjuje ili povećava?

6. Da li je inverzna neparna funkcija parna ili neparna?

7. Kako su raspoređeni grafovi međusobno inverznih funkcija?

4. Prezentacija novog materijala.

1) Koncept invertibilne funkcije. Dovoljan uslov za reverzibilnost.

Na interaktivnoj tabli nastavnik upoređuje grafove dviju funkcija čiji su domeni definicije i skupovi vrijednosti isti, ali je jedna funkcija monotona, a druga nije (slika 2). Dakle, funkcija ima svojstvo koje nije karakteristično za funkciju: bez obzira koji broj iz skupa vrijednosti funkcijef ( x ) uzmite, to je vrijednost funkcije samo u jednoj tački, tako da nastavnik dovodi učenike do koncepta invertibilne funkcije.

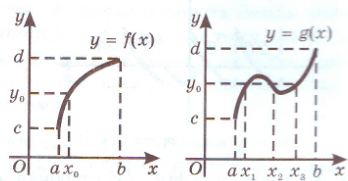
Rice. 2

Nastavnik zatim formulira definiciju inverzibilne funkcije i dokazuje teoremu inverzibilne funkcije koristeći graf monotone funkcije na interaktivnoj tabli.

Definicija 1. Funkcija se pozivareverzibilan , ako uzme bilo koju od svojih vrijednosti samo u jednoj tački skupaX .

Teorema. Ako je funkcija monotona na setuX , tada je reverzibilno.

dokaz:

Neka funkcija y=f(x) povećava na setuX pusti to X 1 ≠x 2 - dva poena setaX .

Za određenost, nekaX 1 < X 2 . Od čega ondaX 1 < X 2 kako se funkcija povećava, slijedi daf(x 1 ) < f(x 2 ) .

Dakle, različite vrijednosti argumenta odgovaraju različita značenja funkcije, tj. funkcija je reverzibilna.

Slično se dokazuje teorema u slučaju opadajuće funkcije.

(Tokom dokazivanja teoreme nastavnik markerom daje sva potrebna objašnjenja na crtežu)

Prije nego što formuliše definiciju inverzne funkcije, nastavnik traži od učenika da odrede koja je od predloženih funkcija reverzibilna? Interaktivna tabla prikazuje grafikone funkcija (sl. 3, 4) i snimljeno je nekoliko analitički specificiranih funkcija:

A ) b )

Rice. 3 Fig. 4

V ) y=2x+5; G ) y = - + 7.

Komentar. Monotonost funkcije jedovoljno uslov za postojanje inverzne funkcije. Ali tonije neophodno stanje.

Nastavnik daje primjere različitih situacija kada funkcija nije monotona već reverzibilna, kada funkcija nije monotona i nije reverzibilna, kada je monotona i reverzibilna.

2) Koncept inverzne funkcije. Algoritam za kompajliranje inverzne funkcije.

Definicija 2. Neka je reverzibilna funkcijay=f(x) definisano na setuX i njegov dometE(f)=Y . Uparimo svakiy od Y onda jedino značenjeX, pri čemu f(x)=y. Tada dobivamo funkciju koja je definirana naY, A X – raspon vrijednosti funkcije. Ova funkcija je označenax=f -1 (y), i nazovi obrnuto s obzirom na funkcijuy=f(x), .

Zatim nastavnik upoznaje učenike sa metodom pronalaženja inverzne funkcije date analitički.

Algoritam za kompajliranje inverzne funkcije za funkciju y = f ( x ), .

Provjerite je li funkcijay=f(x) reverzibilan na intervaluX .

Express varijablaX kroz at iz jednačine y=f(x), uzimajući u obzir to.

U rezultirajućoj jednakosti, zamijeniteX I at. Umjesto x=f -1 (y) pisati y=f -1 (x).

Na konkretnim primjerima nastavnik pokazuje kako se koristi ovaj algoritam.

Primjer 1 Pokažite šta je za funkcijuy=2x-5

Rješenje . Linearna funkcija y=2x-5 odlučno na R, povećava se za R a njegov domet jeR. Dakle, inverzna funkcija postoji naR . Da bismo pronašli njegov analitički izraz, rješavamo jednačinuy=2x-5 relativno X ; dobiti. Preimenujte varijable, dobićemo željenu inverznu funkciju. Definiše se i povećava za R.

Primjer 2 Pokažite šta je za funkcijuy=x 2 , x ≤ 0 postoji inverzna funkcija i pronađite njen analitički izraz.

Rješenje . Funkcija je neprekidna, monotona u svojoj domeni definicije, dakle, invertibilna. Nakon analize domena definicije i skupa vrijednosti funkcije, dolazi se do odgovarajućeg zaključka o analitičkom izrazu za inverznu funkciju, koja ima oblik.

3) Svojstva međusobno inverznih funkcija.

Nekretnina 1. Ako g je funkcija inverzna od f , zatim i f je funkcija inverzna od g (funkcije su međusobno inverzne), dokD ( g )= E ( f ), E ( g )= D ( f ) .

Nekretnina 2. Ako se funkcija povećava (opada) na skupu X, a Y je raspon funkcije, tada se inverzna funkcija povećava (smanjuje) na Y.

Nekretnina 3. Da biste dobili graf funkcije inverzne funkciji, potrebno je transformirati graf funkcije simetrično u odnosu na pravu linijuy=x .

Nekretnina 4. Ako je neparna funkcija invertibilna, onda je i njena inverzna neparna.

Svojstvo 5. Ako funkcije f ( x ) I međusobno inverzno, onda je istinito za bilo koje i istinito za bilo koje.

Primjer 3 Nacrtajte inverznu funkciju ako je moguće.

Rješenje. Ova funkcija nema inverznu u cijelom svom domenu definicije, jer nije monotona. Stoga, razmotrite interval na kojem je funkcija monotona: , dakle, postoji inverz. Hajde da nađemoona . Za ovo izražavamox krozy : . Preimenuj - inverzna funkcija. Napravimo grafove funkcija (slika 5) i uvjerimo se da su simetrični u odnosu na pravu linijuy = x .

Rice. 5

Primjer 4 Pronađite skup vrijednosti svake od međusobno inverznih funkcija, ako to znate.

Rješenje. Prema svojstvu 1 međusobno inverznih funkcija, imamo.

5 . Rezimirajući

Holding dijagnostički rad. Svrha ovog rada je da se utvrdi stepen asimilacije edukativni materijal diskutovano na predavanju. Studenti su pozvani da odgovore na pitanja formulisana na početku predavanja.

6 . inscenacija zadaća.

1. Razumjeti materijal predavanja, naučiti osnovne definicije i formulacije teorema.

2. Dokazati svojstva međusobno inverznih funkcija.

Lekcija 2 Dovoljan uslov za invertibilnost funkcije"

Cilj: formirati sposobnost primjene teorijskih znanja na temu pri rješavanju zadataka, razmotriti glavne vrste problema za proučavanje funkcije za reverzibilnost, za izgradnju inverzne funkcije.

Plan časa radionice:

1. Organizacioni momenat.

2. Aktuelizacija znanja (frontalni rad učenika).

3. Konsolidacija proučenog gradiva (rješavanje problema).

4. Sumiranje lekcije.

5. Izjava o domaćem zadatku.

Tokom nastave.

1. Organiziranje vremena.

Pozdravljanje nastavnika, provjera spremnosti učenika za čas.

2. Ažuriranje znanja. ( prednji rad učenika).

Od učenika se traži da usmeno urade sljedeće zadatke:

1. Formulirajte dovoljan uvjet da funkcija bude invertibilna.

2. Među funkcijama čiji su grafikoni prikazani na slici navedite one koje su reverzibilne.

3. Formulirajte algoritam za kompajliranje funkcije inverzne datoj.

4. Postoje li funkcije inverzne podacima? Ako da, pronađite ih:

A) ; b ) ; c ) .

5. Da li su funkcije čiji su grafovi prikazani na slici međusobno inverzne (slika 6)? Obrazložite odgovor.

Rice. 6

3. Konsolidacija proučenog gradiva (rješavanje problema).

Konsolidacija proučavanog materijala sastoji se od dvije faze:

Pojedinac samostalan rad studenti;

Sumiranje rezultata individualnog rada.

U prvoj fazi učenici dobijaju kartice sa zadacima koje sami izvode.

Vježba 1.

Je li funkcija reverzibilna u cijelom domenu definicije? Ako jeste, onda pronađite obrnuto.

a) ; b) ; c).

Zadatak 2.

Jesu li funkcije međusobno inverzne:

A) ;

b ) .

Zadatak 3.

Razmotrite funkciju na svakom od naznačenih intervala, ako je funkcija invertibilna na ovom intervalu, zatim postavite njen inverz analitički, naznačite domenu definicije i raspon vrijednosti:

a ) R ; b ) ; d ) [-2;0].

Zadatak 4.

Dokažite da je funkcija nepovratna. Nađite funkciju inverznu njoj na intervalu i nacrtajte njen graf.

Zadatak 5.

Nacrtajte funkciju i odredite postoji li za nju inverzna funkcija. Ako da, onda nacrtajte inverznu funkciju na istom crtežu i postavite je analitički:

a ) ; b ) .

U fazi sumiranja rezultata individualnog rada učenika, zadaci se provjeravaju samo uz fiksiranje međurezultata. Problemi koji su izazvali najveće poteškoće razmatraju se na tabli ili uz otkrivanje potrage za rješenjima, ili uz zapis o cjelokupnom rješenju.

4. Sumiranje lekcije (refleksija).

Studentima se nudi mini upitnik:

Šta mi se svidjelo na lekciji?______________________________

Šta mi se nije dopalo na lekciji? ________________________________

_________________________________________________________________

Odaberite jednu izjavu koja vam najviše odgovara:

1) Mogu samostalno istražiti funkciju za reverzibilnost, izgraditi inverz i siguran sam da je rezultat tačan.

2) Mogu ispitati funkciju za reverzibilnost, izgraditi inverz, ali nisam uvijek siguran u ispravnost rezultata, potrebna mi je pomoć mojih drugova.

3) Praktično ne mogu da istražujem funkciju za reverzibilnost, izgradim inverz, treba mi dodatni savet nastavnika.

Gdje mogu primijeniti stečeno znanje?____________________ ________________________________________________________________

5. Postavljanje domaće zadaće.

№ 10.3, 10.6(c, d), 10.7(c, d), 10.9(c, d), 10.13(c, d), 10.18.(Mordkovich, A.G. Algebra i početak matematičke analize 10. razred. U 14:00 2. dio. Zadatak za studente obrazovnih institucija ( nivo profila) / A.G. Mordkovich, P.V. Semenov. - M.: Mnemosyne, 2014. - 384 str.)

I. Saopštavanje teme i svrhe časa

II. Ponavljanje i konsolidacija obrađenog gradiva

1. Odgovori na pitanja o domaćem zadatku (analiza neriješenih problema).

2. Praćenje usvajanja gradiva (samostalni rad).

Opcija 1

Opcija 2

Provedite studiju funkcije i izgradite njen graf:

III. Učenje novog gradiva

Prema analitičkom obliku funkcije, za bilo koju vrijednost argumenta, lako je pronaći odgovarajuću vrijednost funkcije y. Često se javlja inverzni problem: vrijednost y je poznata i potrebno je pronaći vrijednost argumenta x na kojoj se to postiže.

Primjer 1

Pronađite vrijednost argumenta x ako je vrijednost funkcijeje jednako: a) 2; b) 7/6; u 1.

Iz analitičkog oblika funkcijeizraziti varijablu x i dobiti: 4 xy - 2y = 3x + 1 ili x(4y - 3) = 2y + 1, odakle. Sada je lako riješiti problem:

Funkcija naziva se inverzna funkcija. Pošto je uobičajeno da se argument funkcije označava slovom x, a vrijednost funkcije slovom y, inverzna funkcija se piše kao

Dajemo pojmove neophodne za proučavanje teme.

Definicija 1. Funkcija y = f(x), x ∈ X se naziva reverzibilnim ako uzima bilo koju od svojih vrijednosti samo u jednoj točki x skupa X (drugim riječima, ako različite vrijednosti argumenta odgovaraju različitim vrijednostima funkcije). U suprotnom, funkcija se naziva nepovratna.

Primjer 2

Funkcija svaka njegova vrijednost zauzima samo jednu tačku x i reverzibilna je (grafikon a). Funkcijaima takve vrijednosti y (na primjer, y = 2) koje se postižu u dvije različite točke x , i nepovratan je (grafikon b).

Kada se razmatra tema, korisna je sljedeća teorema.

Teorema 1. Ako je funkcija y = f(x), x ∈ X je monoton na skupu X, tada je invertibilan.

Primjer 3

Vratimo se na prethodni primjer. Funkcijaopada (monoton) i inverzibilan je u cijelom domenu definicije. Funkcijanemonotoni i nepovratni. Međutim, ova funkcija raste na intervalima (-∞; -1] i . Stoga je na takvim intervalima funkcija invertibilna. Na primjer, funkcija je invertibilna na segmentu x ∈ [-1; 1].

Definicija 2. Neka je y = f(x), x ∈ X je invertibilna funkcija i E(f) = Y . Uparimo svaki Y jedina vrijednost x za koju f(x ) = y (tj. jedini korijen jednačine f(x ) = y u odnosu na varijablu x). Tada dobivamo funkciju koja je definirana na skupu Y (skup X je njegov opseg). Ova funkcija je označena x - f -1 (y), y ∈ Y i naziva se inverznim u odnosu na funkciju y = f(x), x ∈ X. Slika prikazuje funkciju y = f (x) i inverzna funkcija x \u003d f -1 (y).

Direktne i inverzne funkcije imaju istu monotonost.

Teorema 2. Ako je funkcija y = f (x) raste (smanjuje) na skupu X, a Y je njegov raspon vrijednosti, tada je inverzna funkcija x = f -1 (y ) se povećava (smanjuje) na setu Y .

Primjer 4

Funkcija smanjuje se na setui ima mnogo značenjaInverzna funkcijatakođer se smanjuje na setui ima mnogo značenjaOčigledno, grafovi funkcija I poklapaju, budući da ove funkcije dovode do istog odnosa između varijabli x i y: 4xy - 3x - 2y - 1 = 0.

Kod nas je uobičajeno da se argument funkcije označava slovom x, a vrijednost funkcije slovom y. Stoga ćemo inverznu funkciju napisati u obliku y = f -1 (x) (vidi primjer 1).

Teorema 3. Grafovi funkcije y = f (x) i inverzna funkcija y = f-1 su simetrične u odnosu na relativnu pravu y = x.

Primjer 5

Za funkciju y = 2x - 4 nalazimo inverznu funkciju: y + 4 = 2x, odakle je x = 1/2y + 2. Preimenujmo x↔ y i zapišite inverznu funkciju kao y = 1/2x + 2. Dakle, za funkciju f (x) \u003d 2x - 4 inverzna funkcija f -1 (x ) = 1/2x + 2. Nacrtajmo grafove ovih funkcija. Može se vidjeti da su grafovi simetrični u odnosu na relativnu pravu liniju y = x.

Funkcija f-1(x ) \u003d 1/2x + 2 inverzno u odnosu na funkciju f (x) \u003d 2x - 4. Ali funkcija f (x) = 2x - 4 je inverzna funkcija f -1 (x ) = 1/2x + 2. Dakle, funkcije f(x) i f-1 (x) je ispravnije nazvati recipročnim. U ovom slučaju ispunjene su sljedeće jednakosti: f -1 (f (x)) = x i f (f -1 (x) = x.

IV. Kontrolna pitanja

1. Reverzibilne i nepovratne funkcije.

2. Invertibilnost monotone funkcije.

3. Definicija inverzne funkcije.

4. Monotonost direktnih i inverznih funkcija.

5. Grafovi direktnih i inverznih funkcija.

V. Zadatak u lekciji

§ 3, broj 1 (a, b); 2 (c, d); 3 (a, d); 4 (c, d); 5 (a, c).

VI. Zadaća

§ 3, broj 1 (c, d); 2 (a, b); 3 (b, c); 4 (a, b); 5 (b, d).

VII. Sumiranje lekcije

Ciljevi lekcije:

edukativni:

• izgraditi znanje na nova tema u skladu sa programskim materijalom;
• proučavati svojstvo invertibilnosti funkcije i naučiti kako pronaći funkciju inverznu datoj;

u razvoju:

• razviti vještine samokontrole, predmetni govor;
• savladati koncept inverzne funkcije i naučiti metode pronalaženja inverzne funkcije;

Obrazovni: formirati komunikativnu kompetenciju.

Oprema: kompjuter, projektor, platno, SMART Board interaktivna tabla, materijal (samostalni rad) za grupni rad.

Tokom nastave.

1. Organizacioni momenat.

Target – priprema učenika za rad u učionici:

Definicija odsutnog,

Odnos učenika prema radu, organizacija pažnje;

Poruka o temi i svrsi lekcije.

2. Ažuriranje osnovnih znanja učenika. front poll.

Cilj - utvrditi ispravnost i svijest o proučavanom teorijskom gradivu, ponavljanje obrađenog gradiva.<Приложение 1 >

Grafikon funkcije prikazan je na interaktivnoj tabli za učenike. Nastavnik formuliše zadatak - razmotriti graf funkcije i navesti proučavana svojstva funkcije. Studenti navode svojstva funkcije prema projektu istraživanja. Nastavnik, desno od grafikona funkcije, zapisuje imenovana svojstva markerom na interaktivnoj tabli.

Svojstva funkcije:

Na kraju učenja, nastavnik izvještava da će se danas na času upoznati sa još jednim svojstvom funkcije - reverzibilnošću. Za sadržajno proučavanje novog gradiva, nastavnik poziva djecu da se upoznaju sa glavnim pitanjima na koja učenici moraju odgovoriti na kraju časa. Pitanja su napisana na običnoj tabli i svaki učenik ima materijal (podijeljen prije časa)

1. Šta je reverzibilna funkcija?
2. Je li svaka funkcija reverzibilna?
3. Koja je inverzna data funkcija?
4. Kako su povezani domen definicije i skup vrijednosti funkcije i njene inverzne funkcije?
5. Ako je funkcija data analitički, kako definirati inverznu funkciju s formulom?
6. Ako je funkcija data grafički, kako nacrtati njenu inverznu funkciju?

3. Objašnjenje novog materijala.

Target - formiranje znanja o novoj temi u skladu sa programskim materijalom; proučavati svojstvo invertibilnosti funkcije i naučiti kako pronaći funkciju inverznu datoj; razvijati predmet.

Nastavnik izvodi prezentaciju gradiva u skladu sa materijalom iz stava. Na interaktivnoj tabli nastavnik upoređuje grafove dviju funkcija čiji su domeni definicije i skupovi vrijednosti isti, ali je jedna funkcija monotona, a druga nije, čime učenike dovodi pod koncept invertibilne funkcije. .

Nastavnik zatim formulira definiciju inverzibilne funkcije i dokazuje teoremu inverzibilne funkcije koristeći graf monotone funkcije na interaktivnoj tabli.

Definicija 1: Poziva se funkcija y=f(x), x X reverzibilan, ako uzme bilo koju od svojih vrijednosti samo u jednoj tački skupa X.

Teorema: Ako je funkcija y=f(x) monotona na skupu X, onda je inverzibilna.

dokaz:

1. Neka funkcija y=f(x) povećava za X pusti to x 1 ≠ x 2- dva poena seta X.
2. Za određenost, neka x 1< x 2.
   Od čega onda x 1< x 2 sledi to f(x 1) < f(x 2).
3. Dakle, različite vrijednosti argumenta odgovaraju različitim vrijednostima funkcije, tj. funkcija je reverzibilna.

(Tokom dokazivanja teoreme nastavnik markerom daje sva potrebna objašnjenja na crtežu)

Prije nego što formuliše definiciju inverzne funkcije, nastavnik traži od učenika da odrede koja je od predloženih funkcija reverzibilna? Interaktivna tabla prikazuje grafikone funkcija i napisano je nekoliko analitički definisanih funkcija:

B)

G) y = 2x + 5

D) y = -x 2 + 7

Nastavnik uvodi definiciju inverzne funkcije.

Definicija 2: Neka je invertibilna funkcija y=f(x) definisano na setu X I E(f)=Y. Uparimo svaki y od Y onda jedino značenje X, pri čemu f(x)=y. Tada dobivamo funkciju koja je definirana na Y, A X je opseg funkcije

Ova funkcija je označena x=f -1 (y) i zove se inverzna funkcija y=f(x).

Studenti se pozivaju da donesu zaključak o odnosu između domene definicije i skupa vrijednosti inverznih funkcija.

Da bi razmotrio pitanje kako pronaći inverznu funkciju datog, nastavnik je uključio dva učenika. Dan ranije djeca su od učitelja dobila zadatak da samostalno analiziraju analitičke i grafičke metode za pronalaženje inverzne zadate funkcije. Nastavnik je bio konsultant u pripremi učenika za čas.

Poruka prvog učenika.

Napomena: monotonost funkcije je dovoljno uslov za postojanje inverzne funkcije. Ali to nije neophodno stanje.

Student je naveo primjere različitih situacija kada funkcija nije monotona, već reverzibilna, kada funkcija nije monotona i nije reverzibilna, kada je monotona i reverzibilna

Zatim učenik upoznaje studente sa metodom pronalaženja inverzne funkcije date analitički.

Algoritam pronalaženja

1. Provjerite je li funkcija monotona.
2. Izrazite x u terminima y.
3. Preimenujte varijable. Umjesto x = f -1 (y) pišu y = f -1 (x)

Zatim rješava dva primjera za pronalaženje funkcije inverzne od datog.

Primjer 1: Pokazati da postoji inverzna funkcija za funkciju y=5x-3 i pronaći njen analitički izraz.

Rješenje. Linearna funkcija y=5x-3 je definirana na R, raste na R, a njen raspon je R. Dakle, inverzna funkcija postoji na R. Da bismo pronašli njen analitički izraz, rješavamo jednačinu y=5x-3 u odnosu na x; dobijamo Ovo je željena inverzna funkcija. Definiše se i povećava za R.

Primjer 2: Pokazati da postoji inverzna funkcija za funkciju y=x 2 , x≤0 i pronaći njen analitički izraz.

Funkcija je neprekidna, monotona u svojoj domeni definicije, dakle, invertibilna. Nakon analize domena definicije i skupa vrijednosti funkcije, dolazi se do odgovarajućeg zaključka o analitičkom izrazu za inverznu funkciju.

Drugi učenik pravi prezentaciju o grafički kako pronaći inverznu funkciju. U toku svog objašnjenja učenik koristi mogućnosti interaktivne table.

Da biste dobili grafik funkcije y=f -1 (x), inverzan funkciji y=f(x), potrebno je transformirati graf funkcije y=f(x) simetrično u odnosu na pravu liniju y=x.

Tokom objašnjenja na interaktivnoj tabli izvodi se sljedeći zadatak:

Konstruirajte graf funkcije i graf njene inverzne funkcije u istom koordinatnom sistemu. Zapišite analitički izraz za inverznu funkciju.

4. Primarna fiksacija novog materijala.

Cilj - utvrditi ispravnost i svijest o razumijevanju proučavanog gradiva, uočiti nedostatke u primarnom razumijevanju gradiva, ispraviti ih.

Učenici su podijeljeni u parove. Daju im se listovi sa zadacima u kojima rade u parovima. Vrijeme za završetak radova je ograničeno (5-7 minuta). Jedan par učenika radi na računaru, projektor je za ovo vrijeme isključen, a ostala djeca ne mogu vidjeti kako učenici rade na računaru.

Na kraju vremena (pretpostavlja se da je većina učenika završila rad), interaktivna tabla (projektor se ponovo uključuje) prikazuje rad učenika, pri čemu se tokom testa pojašnjava da je zadatak obavljen u parovi. Po potrebi nastavnik vrši korektivni, objašnjavajući rad.

Samostalni rad u parovima<Aneks 2 >

5. Rezultat lekcije. Na pitanja koja su postavljena prije predavanja. Objava ocjena za čas.

Domaći zadatak §10. №№ 10.6(a,c) 10.8-10.9(b) 10.12(b)

Algebra i počeci analize. 10. razred U 2 dijela za obrazovne ustanove (nivo profila) / A.G. Mordkovich, L.O. Denishcheva, T.A. Koreshkova i drugi; ed. A.G. Mordkovich, M: Mnemosyne, 2007

Inverzna funkcija

Tekst lekcije

• Apstraktna lekcija 1-3 (Morozova I. A.)

  Naziv predmeta Algebra i početak matematičke analize Razred 10 UMK Algebra i početak matematičke analize. 10-11 razredi. U 2 sata Dio 1. Udžbenik za studente obrazovnih ustanova ( osnovni nivo)/ A.G. Mordkovich. - 10. izd., Sr. - M.: Mnemozina, 2012. Dio 2. Zadatak za studente obrazovnih ustanova (osnovni nivo) / [A.G. Mordkovich i drugi]; ed. A.G. Mordkovich. - 10. izd., Sr. - M.: Mnemosyne, 2012. Stepen obrazovanja je osnovni Tema časa: Inverzna funkcija. (3 sata) Lekcija 1. Svrha časa: upoznati pojmove reverzibilnih i inverznih funkcija; dokazati teoremu o monotonosti direktnih i inverznih funkcija; identifikovati i opravdati geometrijsko značenje reverzibilnost funkcije Ciljevi časa: - formirati sposobnost pronalaženja inverzne funkcije za datu; - formirati sposobnost izgradnje grafa inverzne funkcije. Očekivani rezultati: Znati: definiciju inverzne funkcije, inverznu funkciju, znak reverzibilnosti funkcije. Biti sposoban: pronaći formulu funkcije inverzne datoj; izgraditi graf inverzne funkcije koristeći graf ove funkcije. Tehnička podrška nastavnog računara, platna, projektora, udžbenika. Tok časa I. Organizacioni momenat. II. Provjera domaćih zadataka (analiza zadataka koji su učenicima stvarali poteškoće) III. Posao verifikacije. Opcija 1 1. Zadata je funkcija a) Ispitati monotonost funkcije ako je x > 2. b) Naći najveću i najmanju vrijednost funkcije na segmentu [–1,5; 1.5]. 2. Ispitati ograničenost funkcije gdje je x > 0. 3. Ispitajte funkciju na paritet. Opcija 2 1. Zadana funkcija a) Ispitati monotonost funkcije ako je x< 2. б) Найдите наибольшее и наименьшее значения функции на отрезке [–4,5; –3,1]. 2. Исследуйте функцию где х < 0, на ограниченность. 3. Исследуйте функцию на четность. Вариант 3 1. Дана функция а) Исследуйте функцию на монотонность, если х < –1. б) Найдите наибольшее и наименьшее значения функции на отрезке [–2; 0,4]. 2. Исследуйте функцию где х < –1, на ограниченность. 3. Исследуйте функцию на четность. Вариант 4 1. Дана функция а) Исследуйте функцию на монотонность, если х  1. б) Найдите наибольшее и наименьшее значения функции на отрезке . 2. Исследуйте функцию где х >2, za ograničenje. 3. Ispitajte funkciju na paritet. Rješenje opcija 1 i 3 verifikacionog rada. Opcije 1 i 2 su nešto lakše od opcija 3 i 4. Opcija 1 1. Označite a) Zatim neka funkcija opada na (–; 2]. b) Pošto funkcija opada na (–∞; 2], onda je odgovor : a) smanjuje; b) unaib. = 12,25; unaim. = 0,25. 2. gdje je x > 0. Funkcija je odozgo ograničena pravom linijom y = 0, što znači da je funkcija odozgo ograničena pravom linijom y = 1. Odgovor: ograničena odozgo. 3. - simetrično u odnosu na ishodište. pa je funkcija neparna. Odgovor: čudno. Opcija 3 1. a) Označite Graf je parabola sa vrhom u tački (–1; –1) i siječe osu 0x u tačkama x = 0 i x = –2. Ako je x > -1, tada se funkcija povećava. b) Na intervalu [–2; 0,4] i odgovor: a) povećava; b) unaib. = 0,96; unaim. = 0. 2. gdje je x< –1. Функция ограничена снизу прямой у = 0, значит, функция ограничена снизу прямой у = 2. Ответ: ограничена снизу. 3. – симметрична относительно начала координат. Если х = 0, то Имеем: значит, функция ни четная, ни нечетная. Ответ: ни четная, ни нечетная. IV. Объяснение нового материала. 1. Для введения понятия обратимой функции можно использовать либо подвижные модели, либо изображение обратимых и необратимых функций на прозрачной пленке, перевернув которую можно показать, как область определения и область значения функции «меняются местами» и в каком случае обеспечивается однозначность обратной функции. 2. Для первичного закрепления материала учащиеся выполняют следующее задание. Среди функций, графики которых изображены на рисунке, укажите обратимые. 3. Теорема 1. Подчеркиваем учащимся, что в теореме сформулирован признак обратимости функции (достаточное условие). В то же время монотонность не является необходимым условием обратимости. Динамическая пауза. V. Формирование умений и навыков. Упражнения, решаемые на этом уроке, направлены на аналитическое задание функции, обратной данной. № 3.1 (а; б), № 3. 2 (а; б). При выполнении этих упражнений следует предупредить формализм в аналитическом задании функции путем простого преобразования уравнения. Учащиеся должны обосновать существование обратной функции. Решение: № 3.1 (б). Линейная функция у = 2 + 4х определена на R, возрастает на R(k  0), E(f) = R. Значит, на R существует обратная функция. – искомая обратная функция, возрастающая на R. Ответ: № 3.2 (б). Функция убывает на всей области определения, значит, существует обратная функция, определенная и убывающая на Ответ: V. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. Домашнее задание: № 3.1 (в; г) – № 3.2 (в; г). Урок 2. Цель урока: выявить и обосновать геометрический смысл обратимости функции Задачи урока: - развивать умение находить обратную функцию для заданной; - формировать умение строить график обратной функции. Планируемые результаты: Знать: определение обратимой функция, обратной функции, признак обратимости функции. Уметь: находить формулу функции, обратной данной; строить график обратной функции, используя график данной функции. Техническое обеспечение урока компьютер, экран, проектор, учебник. Ход урока I. Организационный момент. II. Проверка домашнего задания (разбор заданий, вызвавших затруднения учащихся) III. Работа в группах. Карточка 1. Карточка 2. IV. Объяснение нового материала. Устанавливая геометрический смысл обратимости функции, учащиеся формулируют способ построения графика обратной функции с помощью преобразования осевой симметрии. Графики функции у = f(х) и обратной функции у = f-1 симметричны относительной прямой у = х. Для функции у = 2х - 4 найдем обратную функцию: у + 4 = 2х, откуда х = 1/2у + 2. Введем переобозначения х ↔ у и запишем обратную функцию в виде у = 1/2х + 2. Таким образом, для функции f(х) = 2х – 4 обратная функция f-1(x) = 1/2х + 2. Построим графики этих функций. Видно, что графики симметричны относительной прямой у = х. Функция f-1(x) = 1/2х + 2 обратная по отношению к функции f(х) = 2х - 4. Но и функция f(х) = 2х - 4 является обратной по отношению к функции f-1(x) = 1/2х + 2. Поэтому функции f(х) и f-1(х) корректнее называть взаимообратными. При этом выполнены равенства: f-1(f(х)) = х и f(f-1(x) = x. Динамическая пауза. V. Формирование умений и навыков. Упражнения, решаемые на этом уроке, направлены на построение графика обратной функции с помощью осевой симметрии. № 3.3 (а; б), № 3. 4 (а; б), № 3.5* (а; б). Решение: № 3. 4 (б). Графиком является кубическая парабола, полученная из графика у = х3 сдвигом вправо по оси 0х на 2 единицы. Функция возрастает на R, значит, существует обратная функция, заданная и возрастающая на R. Ответ: V. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. – Каков характер монотонности прямой и обратной функций? – Как построить график обратной функции, используя график данной функции? Домашнее задание: № 3.3 (в; г) – № 3.4 (в; г) № 3.5 * (в; г) – по желанию. Урок 3. Цель урока: проверить степень усвоения теоретического материала и умения применять его при выполнении письменной работы Задачи урока: - развивать умение находить обратную функцию для заданной; - развивать умение строить график обратной функции. Планируемые результаты: Знать: определение обратимой функция, обратной функции, признак обратимости функции. Уметь: находить формулу функции, обратной данной; строить график обратной функции, используя график данной функции. Техническое обеспечение урока компьютер, экран, проектор, учебник. Ход урока I. Организационный момент. II. Проверка домашнего задания (разбор заданий, вызвавших затруднения учащихся) III. Зачетная работа Вариант 1. Вариант 2. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. – Каков характер монотонности прямой и обратной функций? – Как построить график обратной функции, используя график данной функции? Домашнее задание: §3, примеры 1-3.

  Preuzmi: Algebra 10kl - Apstraktna lekcija 1-3 (Morozova I. A.).docx

• lekcija 1 (Samoilova G.A.)

  Algebra i počeci analize 10. razred TMC: Algebra i počeci analize 10.-11. razred, A.G. Mordkovich, Moskva 2013. Nivo učenja: osnovni Tema: Inverzna funkcija Ukupno sati: 3 sata Na temu: Lekcija br. 1 Svrha časa: Obrazovna: Uvesti i učvrstiti definiciju inverzne funkcije; proučavati svojstvo invertibilnosti funkcije i naučiti kako pronaći funkciju inverznu datoj; Razvijanje: razvijanje vještina samokontrole, predmetnog govora; savladati koncept inverzne funkcije i naučiti metode pronalaženja inverzne funkcije; Obrazovni: formirati komunikativnu kompetenciju. Ciljevi časa: 1. Upoznati učenike sa reverzibilnim funkcijama i njihovim grafovima. 2.Obogatiti iskustvo studenata u sticanju novih znanja na osnovu postojećih teorijskih znanja, kao i korišćenjem poznatih praktičnih situacija Očekivani rezultati: Nakon proučavanja ove teme studenti treba da znaju: Definiciju reverzibilne funkcije; crtanje reverzibilne funkcije; primjeri funkcija iz života; metode poređenja, generalizacije, sposobnost izvođenja zaključaka; Nakon proučavanja ove teme, studenti treba da budu sposobni da: samostalno dopune i sistematizuju svoja znanja: -izgrade grafove reverzibilnih funkcija: -umeju da donose zaključke. Tehnička podrška lekcije: tutorial Algebra i počeci analize. 10. razred (osnovni nivo) „A.G. Mordkovich. stolovi numeričke funkcije . Računar, projektor, platno. Dodatna metodičko-didaktička podrška času: Metodički vodič za nastavnike „Planovi časova za udžbenik Algebra i početak analize 10-11. razred“, A.G. Mordkovich, Volgograd 2013. Internet resursi https:// 1september.ru Sadržaj časa: 1. Organizacioni momenat 2. Kontrola preostalog znanja 3. Učenje novog materijala 4. Konsolidacija 5. Sažetak lekcije 6. Postavljanje domaće zadaće Tok časa: 1 Organizacioni momenat 2 .Kontrola rezidualnog znanja 1). Ponavljanje i učvršćivanje obrađenog gradiva 1. Odgovori na pitanja o domaćem zadatku (analiza neriješenih zadataka). 2. Praćenje usvajanja gradiva (samostalni rad). Opcija 1. Proučiti funkciju i izgraditi njen graf: 3. Učenje novog materijala Prema analitičkom obliku funkcije za bilo koju vrijednost argumenta, lako je pronaći odgovarajuću vrijednost funkcije y. Često se javlja inverzni problem: vrijednost y je poznata i potrebno je pronaći vrijednost argumenta x za koji se ona postiže. Primjer 1 Pronađite vrijednost argumenta x ako je vrijednost funkcije: a) 2; b) 7/6; c) 1. Iz analitičkog oblika funkcije izražavamo varijablu x i dobijamo: 4xy - 2y = 3x + 1 ili x (4y - 3) = 2y + 1, odakle. Sada je lako riješiti problem: funkcija se zove inverzna funkciji. Budući da je uobičajeno da se argument funkcije označava slovom x, a vrijednost funkcije slovom y, inverzna funkcija se piše u obliku Dajemo pojmove potrebne za proučavanje teme. Definicija 1. Funkcija y = f(x), x ∈ X naziva se invertibilnom ako uzima bilo koju od svojih vrijednosti samo u jednoj tački x skupa X (drugim riječima, ako odgovaraju različite vrijednosti funkcije na različite vrijednosti argumenta). U suprotnom, funkcija se naziva nepovratna. Primjer 2 Funkcija uzima svaku od svojih vrijednosti samo u jednoj tački x i reverzibilna je (grafikon a). Funkcija ima takve vrijednosti y (na primjer, y = 2), koje se postižu u dvije različite točke x, i nepovratna je (grafikon b). Kada se razmatra tema, korisna je sljedeća teorema. Teorema 1. Ako je funkcija y = f(x), ∈ monotona na skupu X, onda je invertibilna. Primjer 3 Vratimo se na prethodni primjer. Funkcija opada (monotona) i inverzibilna je u cijeloj domeni definicije. Funkcija je nemonotona i nepovratna. Međutim, ova funkcija raste na intervalima (-∞; -1] i . Stoga je na takvim intervalima funkcija invertibilna. Na primjer, funkcija je invertibilna na segmentu x [-1; 1]. Definicija 2. Neka je y \u003d f (x), x ∈ X je invertibilna funkcija i E(f) = Y. Dodijelimo svakom Y jedinstvenu vrijednost x za koju je f(x) = y (tj. tj. jedini korijen jednadžbe f(x) = y u odnosu na varijablu x). Tada dobijamo funkciju koja je definirana na skupu Y (skup X je njegov raspon vrijednosti). Ova funkcija je označena x - f-1(y), y ∈ Y i naziva se inverzna u odnosu na funkciju y = f(x), x ∈ X. Na slici je prikazana funkcija y = f(x) i inverzna funkcija funkcija x = f- 1(y). Direktne i inverzne funkcije imaju istu monotonost. Teorema 2. Ako se funkcija y = f (x) povećava (smanjuje) na skupu X, a Y je njen raspon, tada se inverzna funkcija x = f-1 (y) povećava (smanjuje) na skupu Y. Primjer 4 Funkcija se smanjuje na skupu i ima skup vrijednosti Inverzna funkcija se također smanjuje na skupu i ima skup vrijednosti Očigledno, grafovi funkcija i poklapaju se, budući da ove funkcije dovode do istog odnosa između varijable x i y: 4xy - 3x - 2y - 1 = 0. Kod nas je uobičajeno da se argument funkcije označava slovom x, vrijednost funkcije - slovom y. Stoga ćemo inverznu funkciju napisati u obliku y = f-1 (x) (vidi primjer 1). Teorema 3. Grafovi funkcije y = f (x) i inverzne funkcije y = f-1 simetrični su relativnoj pravoj liniji y = x. Primjer 5 Za funkciju y = 2x - 4 nalazimo inverznu funkciju: y + 4 = 2x, od čega je x = 1/2y + 2. Uvodimo preimenovanje x ↔ y i upisujemo inverznu funkciju u oblik y \u003d 1/2x + 2. Dakle, za funkciju f(x) = 2x - 4, inverzna funkcija f-1(x) = 1/2x + 2. Napravimo grafove ovih funkcija. Može se vidjeti da su grafovi simetrični u odnosu na relativnu pravu liniju y = x. Funkcija f-1 (x) = 1/2x + 2 je inverzna u odnosu na funkciju f (x) = 2x - 4. Ali funkcija f (x) = 2x - 4 je također inverzna u odnosu na funkciju f -1 (x) \u003d 1/2x + 2. Stoga se funkcije f (x) i f-1 (x) pravilnije nazivaju međusobno inverznim. U ovom slučaju su ispunjene sljedeće jednakosti: f-1 (f (x)) = x i f (f-1 (x) = x. 4. Konsolidacija 1) Kontrolna pitanja: 1. Reverzibilne i nepovratne funkcije. 2. Invertibilnost monotone funkcije. 3. Definicija inverzne funkcije. 4. Monotonost direktnih i inverznih funkcija. 5. Grafovi direktnih i inverznih funkcija. 2) Zadatak na času § 3, br. 1 (a, b); 2 (c, d); 3 (a, d); 4 (c, d); 5 (a, c). 5. Sažetak lekcije Šta ste novo naučili na lekciji danas? Na koje ste teškoće nailazili? Donesite zaključak o odnosu između domene definicije i skupa vrijednosti inverznih funkcija. 4. Izjava o domaćem zadatku § 3, br. 1 (c, d); 2 (a, b); 3 (b, c); 4 (a, b); 5 (b, d).

  Preuzmi: Algebra 10kl - lekcija 1 (Samoilova G. A.).doc

• lekcija 2 (Samoilova G.A.)

  Algebra i počeci analize 10. razred TMC: Algebra i počeci analize 10.-11. razred, A.G. Mordkovich, Moskva 2013 Nivo učenja: osnovni Tema: Inverzna funkcija Ukupno sati: 3 Na temu: čas br. 2 Cilj časa: Obrazovni: utvrditi definiciju inverzne funkcije; konsolidirati znanja o svojstvima invertibilnosti funkcije i naučiti kako pronaći funkciju inverznu datoj; Razvijanje: razvijanje vještina samokontrole, predmetnog govora; vlastite metode pronalaženja inverzne funkcije; Obrazovni: formirati komunikativnu kompetenciju; Organizirati problemsko-tragački rad učenika Ciljevi časa: 1. Upoznati učenike sa reverzibilnim funkcijama i njihovim grafovima. 2.Obogatiti iskustvo studenata u sticanju novih znanja na osnovu postojećih teorijskih znanja, kao i korišćenjem poznatih praktičnih situacija Očekivani rezultati: Nakon proučavanja ove teme studenti treba da znaju: Definiciju reverzibilne funkcije; crtanje reverzibilne funkcije; primjeri funkcija iz života; metode poređenja, generalizacije. Nakon proučavanja ove teme, studenti bi trebali biti sposobni: - samostalno dopuniti i sistematizovati svoja znanja; - graditi grafove reverzibilnih funkcija; - biti sposobni da izvode zaključke. Tehnička podrška časa: udžbenik „Algebra i početak analize. 10. razred (osnovni nivo) „A.G. Mordkovich. Tablice numeričkih funkcija. Računar, projektor, platno. Dodatna metodičko-didaktička podrška času: Metodički vodič za nastavnike „Planovi časova za udžbenik Algebra i početak analize 10-11. razred“, A.G. Mordkovich, Volgograd 2013. Internet resursi https:// 1september.ru Sadržaj časa: 1. Organizacioni trenutak 2. Provera domaćeg zadatka 3. Konsolidacija proučenog materijala 4. Testiranje 5. Rezime časa 6. Postavljanje domaćeg zadatka 1. Organizacioni trenutak. Nastavnik govori učenicima temu, svrhu časa i sredstva za postizanje iste. 2. Provjera domaćeg zadatka 1) Zadatke koji su izazvali poteškoće rješavamo na tabli 2) Frontalni pregled teorijskog dijela teme Pitanja: 1. Koja funkcija se zove reverzibilna? 2. Da li je bilo koja funkcija reverzibilna? 3. Koja se funkcija naziva inverzno data? 4. Kako su povezani domen definicije i skup vrijednosti funkcije i njene inverzne funkcije? 5. Ako je funkcija data analitički, kako definirati inverznu funkciju s formulom? 6. Ako je funkcija data grafički, kako nacrtati njenu inverznu funkciju? 3. Učvršćivanje proučenog gradiva 1) Rad na gotovom crtežu (ponavljanje svojstava numeričke funkcije). Grafikon funkcije prikazan je na interaktivnoj tabli za učenike. Nastavnik formuliše zadatak - razmotriti graf funkcije i navesti proučavana svojstva funkcije. Studenti navode svojstva funkcije prema projektu istraživanja. Učenik desno od grafikona funkcije zapisuje imenovana svojstva markerom na interaktivnoj tabli. Svojstva funkcije: 1. D(f) = [-4;),E(y) = i na i na [-1;0] 6. ymax- ne postoji ymin=0 pri x=0 7. xmax= - 1 ,ymax = 2 xmin = -2, ymin = 1 xmin = 0, ymin = 0 8. Konveksno prema dolje za , konveksno prema gore za . 2) Razmotrite funkciju, pronađite joj inverznu vrijednost. (Rad za tablom, upis u svesku). Zadana funkcija y=x2,x∈)