Lektion och presentation på ämnet: "Talsekvenser. Geometrisk progression"
Ytterligare material
Kära användare, glöm inte att lämna dina kommentarer, feedback, förslag! Allt material kontrolleras av ett antivirusprogram.
Läromedel och simulatorer i webbutiken "Integral" för årskurs 9
Effekter och rötter Funktioner och grafer
Killar, idag ska vi bekanta oss med en annan typ av progression.
Ämnet för dagens lektion är geometrisk progression.
Geometrisk progression
Definition. En numerisk sekvens där varje term, med början från den andra, är lika med produkten av den föregående och något fast tal, kallas en geometrisk progression.Låt oss definiera vår sekvens rekursivt: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
där b och q är vissa givna tal. Talet q kallas fortskridandets nämnare.
Exempel. 1,2,4,8,16... Geometrisk progression, där den första delen är lika med en och $q=2$.
Exempel. 8,8,8,8... En geometrisk progression vars första term är åtta,
och $q=1$.
Exempel. 3,-3,3,-3,3... En geometrisk progression vars första term är tre,
och $q=-1$.
Den geometriska progressionen har egenskaperna monotoni.
Om $b_(1)>0$, $q>1$,
då ökar sekvensen.
Om $b_(1)>0$, $0 Sekvensen betecknas vanligtvis som: $b_(1), b_(2), b_(3), ..., b_(n), ...$.
Liksom i aritmetisk progression, om antalet element är ändligt i en geometrisk progression, så kallas progressionen en finit geometrisk progression.
$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Observera att om sekvensen är en geometrisk progression, så är sekvensen av kvadratiska termer också en geometrisk progression. Den andra sekvensen har den första termen $b_(1)^2$ och nämnaren $q^2$.
Formel för den n:e medlemmen av en geometrisk progression
Geometrisk progression kan också specificeras i analytisk form. Låt oss se hur man gör det:$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
Vi kan enkelt se mönstret: $b_(n)=b_(1)*q^(n-1)$.
Vår formel kallas "formel för den n:te medlemmen av en geometrisk progression".
Låt oss gå tillbaka till våra exempel.
Exempel. 1,2,4,8,16... En geometrisk progression vars första term är lika med en,
och $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.
Exempel. 16,8,4,2,1,1/2... En geometrisk progression vars första term är sexton och $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.
Exempel. 8,8,8,8... En geometrisk progression där den första termen är åtta och $q=1$.
$b_(n)=8*1^(n-1)=8$.
Exempel. 3,-3,3,-3,3... En geometrisk progression vars första term är tre och $q=-1$.
$b_(n)=3*(-1)^(n-1)$.
Exempel. Givet en geometrisk progression $b_(1), b_(2), …, b_(n), … $.
a) Det är känt att $b_(1)=6, q=3$. Hitta $b_(5)$.
b) Det är känt att $b_(1)=6, q=2, b_(n)=768$. Hitta n.
c) Det är känt att $q=-2, b_(6)=96$. Hitta $b_(1)$.
d) Det är känt att $b_(1)=-2, b_(12)=4096$. Hitta q.
Lösning.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$ sedan $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.
Exempel. Skillnaden mellan den sjunde och femte medlemmen av den geometriska progressionen är 192, summan av den femte och sjätte delen av progressionen är 192. Hitta den tionde medlemmen av denna progression.
Lösning.
Vi vet att: $b_(7)-b_(5)=192$ och $b_(5)+b_(6)=192$.
Vi vet också: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Sedan:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
Vi har ett ekvationssystem:
$\begin(cases)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(cases)$.
Genom att likställa får våra ekvationer:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Vi har två lösningar q: $q_(1)=2, q_(2)=-1$.
Ersätt successivt i den andra ekvationen:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ inga lösningar.
Vi fick det: $b_(1)=4, q=2$.
Låt oss hitta den tionde termen: $b_(10)=b_(1)*q^9=4*2^9=2048$.
Summan av en ändlig geometrisk progression
Antag att vi har en ändlig geometrisk progression. Låt oss, liksom för en aritmetisk progression, beräkna summan av dess medlemmar.Låt en ändlig geometrisk progression ges: $b_(1),b_(2),...,b_(n-1),b_(n)$.
Låt oss introducera notationen för summan av dess termer: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
I fallet när $q=1$. Alla medlemmar av den geometriska progressionen är lika med den första medlemmen, då är det uppenbart att $S_(n)=n*b_(1)$.
Betrakta nu fallet $q≠1$.
Multiplicera beloppet ovan med q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Notera:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.
$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2) )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.
$S_(n)(q-1)=b_(n)*q-b_(1)$.
$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.
$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.
Vi har fått formeln för summan av en ändlig geometrisk progression.
Exempel.
Hitta summan av de första sju termerna i en geometrisk progression vars första term är 4 och nämnaren är 3.
Lösning.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.
Exempel.
Hitta den femte medlemmen av den geometriska progressionen, som är känd: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.
Lösning.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.
$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
$-4095(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
$341q=1364$.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.
Karakteristisk egenskap hos en geometrisk progression
Killar, med tanke på en geometrisk progression. Låt oss betrakta dess tre på varandra följande medlemmar: $b_(n-1),b_(n),b_(n+1)$.Vi vet det:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Sedan:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
Om progressionen är finit, gäller denna likhet för alla termer utom den första och den sista.
Om det inte är känt i förväg vilken typ av sekvens sekvensen har, men det är känt att: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Då kan vi lugnt säga att detta är en geometrisk progression.
En talsekvens är en geometrisk progression endast när kvadraten på var och en av dess termer är lika med produkten av dess två angränsande termer av progressionen. Glöm inte att för en ändlig progression är detta villkor inte uppfyllt för den första och sista terminen.
Låt oss titta på denna identitet: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ kallas det geometriska medelvärdet av a och b.
Modulen för varje medlem av en geometrisk progression är lika med det geometriska medelvärdet av de två delarna intill den.
Exempel.
Hitta x så att $x+2; 2x+2; 3x+3$ var tre på varandra följande medlemmar av en geometrisk progression.
Lösning.
Låt oss använda den karakteristiska egenskapen:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ och $x_(2)=-1$.
Ersätt sekventiellt i det ursprungliga uttrycket, våra lösningar:
Med $x=2$ fick vi sekvensen: 4;6;9 är en geometrisk progression med $q=1,5$.
Med $x=-1$ fick vi sekvensen: 1;0;0.
Svar: $x=2.$
Uppgifter för självständig lösning
1. Hitta den åttonde första medlemmen av den geometriska progressionen 16; -8; 4; -2 ....2. Hitta den tionde medlemmen av den geometriska progressionen 11,22,44….
3. Det är känt att $b_(1)=5, q=3$. Hitta $b_(7)$.
4. Det är känt att $b_(1)=8, q=-2, b_(n)=512$. Hitta n.
5. Hitta summan av de första 11 medlemmarna av den geometriska progressionen 3;12;48….
6. Hitta x så att $3x+4; 2x+4; x+5$ är tre på varandra följande medlemmar av en geometrisk progression.
Så låt oss sätta oss ner och börja skriva några siffror. Till exempel:
Du kan skriva vilka siffror som helst, och det kan vara hur många som helst (i vårt fall dem). Oavsett hur många siffror vi skriver kan vi alltid säga vilket av dem som är det första, vilket är det andra och så vidare till det sista, det vill säga vi kan numrera dem. Detta är ett exempel på en nummersekvens:
Numerisk sekvensär en uppsättning nummer som vart och ett kan tilldelas ett unikt nummer.
Till exempel för vår sekvens:
Det tilldelade numret är specifikt för endast ett sekvensnummer. Det finns med andra ord inga tresekundersnummer i sekvensen. Det andra numret (som det -th talet) är alltid detsamma.
Numret med numret kallas den -:e medlemmen av sekvensen.
Vi brukar kalla hela sekvensen för någon bokstav (till exempel), och varje medlem av denna sekvens - samma bokstav med ett index som är lika med numret på denna medlem: .
I vårat fall:

De vanligaste typerna av progression är aritmetiska och geometriska. I det här ämnet kommer vi att prata om den andra typen - geometrisk progression.
Varför behöver vi en geometrisk progression och dess historia.
Även i forntiden tog den italienske matematikern, munken Leonardo av Pisa (mer känd som Fibonacci), hand om handelns praktiska behov. Munken ställdes inför uppgiften att bestämma vad som är det minsta antalet vikter som kan användas för att väga godset? I sina skrifter bevisar Fibonacci att ett sådant viktsystem är optimalt: Detta är en av de första situationerna där människor var tvungna att hantera en geometrisk progression, som du säkert har hört talas om och åtminstone har en allmän uppfattning om. När du väl förstår ämnet, fundera på varför ett sådant system är optimalt?
För närvarande, i livets praktik, manifesteras en geometrisk progression när man investerar pengar i en bank, när räntan debiteras på det belopp som ackumulerats på kontot för föregående period. Med andra ord, om du lägger pengar på en tidsbunden insättning i en sparbank, så kommer insättningen om ett år att öka med från det ursprungliga beloppet, d.v.s. det nya beloppet blir lika med bidraget multiplicerat med. Om ytterligare ett år kommer detta belopp att öka med, d.v.s. det belopp som erhållits vid den tidpunkten multipliceras igen med och så vidare. Liknande situation beskrivs i uppgifterna för beräkning av s.k ränta på ränta- procentsatsen tas varje gång från det belopp som står på kontot med hänsyn tagen till tidigare ränta. Vi kommer att prata om dessa uppgifter lite senare.
Det finns många fler enkla fall där en geometrisk progression tillämpas. Till exempel spridningen av influensa: en person infekterade en person, de i sin tur infekterade en annan person, och därmed är den andra vågen av infektion en person, och de i sin tur infekterade en annan ... och så vidare .. .
Förresten, den finansiella pyramiden, samma MMM, är en enkel och torr beräkning enligt egenskaperna hos en geometrisk progression. Intressant? Låt oss ta reda på det.
Geometrisk progression.
Låt oss säga att vi har numerisk sekvens:
Du kommer omedelbart att svara att det är enkelt och namnet på en sådan sekvens är med skillnaden mellan dess medlemmar. Vad sägs om något sånt här:

Om du subtraherar föregående tal från nästa tal, kommer du att se att varje gång du får en ny skillnad (och så vidare), men sekvensen finns definitivt och är lätt att märka - varje efterföljande tal är gånger större än det föregående !

Denna typ av sekvens kallas geometrisk progression och är markerad.
En geometrisk progression ( ) är en numerisk sekvens, vars första term skiljer sig från noll, och varje term, med början från den andra, är lika med den föregående, multiplicerad med samma tal. Detta tal kallas nämnaren för en geometrisk progression.
Begränsningarna att den första termen ( ) inte är lika och inte är slumpmässiga. Låt oss säga att det inte finns några, och den första termen är fortfarande lika, och q är, hmm .. låt, då visar det sig:
Håller med om att detta inte är någon utveckling.
Som du förstår kommer vi att få samma resultat om det är något annat tal än noll, men. I dessa fall kommer det helt enkelt inte att ske någon progression, eftersom hela nummerserien kommer att vara antingen alla nollor, eller ett nummer, och alla övriga nollor.
Låt oss nu prata mer i detalj om nämnaren för en geometrisk progression, det vill säga ca.
Återigen, detta är numret hur många gånger ändras varje efterföljande term geometrisk progression.
Vad tror du att det kan vara? Det stämmer, positivt och negativt, men inte noll (vi pratade om detta lite högre).
Låt oss säga att vi har en positiv. Låt i vårt fall, a. Vad är den andra termen och? Du kan enkelt svara på det:
Okej. Följaktligen, om, så har alla efterföljande medlemmar av progressionen samma tecken - de positiv.
Tänk om det är negativt? Till exempel, en. Vad är den andra termen och?
Det är en helt annan historia
Försök att räkna löptiden för denna progression. Hur mycket fick du? Jag har. Således, om, så växlar tecknen på termerna för den geometriska progressionen. Det vill säga, om du ser en progression med alternerande tecken i dess medlemmar, så är dess nämnare negativ. Denna kunskap kan hjälpa dig att testa dig själv när du löser problem i detta ämne.
Låt oss nu öva lite: försök att avgöra vilka numeriska sekvenser som är en geometrisk progression och vilka som är aritmetiska:
Jag fattar? Jämför våra svar:
- Geometrisk progression - 3, 6.
- Aritmetisk progression - 2, 4.
- Det är varken en aritmetisk eller en geometrisk progression - 1, 5, 7.
Låt oss återgå till vår senaste utveckling, och låt oss försöka hitta dess term på samma sätt som i aritmetiken. Som du kanske har gissat finns det två sätt att hitta den.
Vi multiplicerar successivt varje term med.
Så den -e medlemmen av den beskrivna geometriska progressionen är lika med.
Som du redan gissar kommer du nu själv att härleda en formel som hjälper dig att hitta vilken medlem som helst i en geometrisk progression. Eller har du redan tagit fram det själv och beskrivit hur man hittar den e medlemmen i etapper? Om så är fallet, kontrollera att ditt resonemang är korrekt.
Låt oss illustrera detta med exemplet att hitta den -e medlemmen i denna progression:

Med andra ord:
Ta reda på värdet av en medlem av en given geometrisk progression.
Hände? Jämför våra svar:
Var uppmärksam på att du fick exakt samma nummer som i den föregående metoden, när vi successivt multiplicerade med varje tidigare medlem av den geometriska progressionen.
Låt oss försöka "avpersonifiera" denna formel - vi tar den till en allmän form och får:
Den härledda formeln är sann för alla värden - både positiva och negativa. Kontrollera det själv genom att beräkna villkoren för en geometrisk progression med följande villkor: , a.
Har du räknat? Låt oss jämföra resultaten:
Håller med om att det skulle gå att hitta en medlem av progressionen på samma sätt som en medlem, dock finns det en risk för felräkning. Och om vi redan har hittat den : e termen för en geometrisk progression, a, vad kan då vara lättare än att använda den "stympade" delen av formeln.
En oändligt minskande geometrisk progression.
På senare tid talade vi om vad som kan vara antingen större eller mindre än noll, men det finns speciella värden för vilka den geometriska progressionen kallas minskar oändligt.
Varför tror du att den har ett sådant namn?
Till att börja med, låt oss skriva ner lite geometrisk progression bestående av medlemmar.
Låt oss säga då:
Vi ser att varje efterföljande term är mindre än den föregående i tider, men kommer det att finnas något antal? Du kommer genast att svara "nej". Det är därför det oändligt minskande - minskar, minskar, men aldrig blir noll.
För att tydligt förstå hur detta ser ut visuellt, låt oss försöka rita en graf över vår utveckling. Så för vårt fall har formeln följande form:
På listorna är vi vana vid att bygga beroende av, därför:
Kärnan i uttrycket har inte förändrats: i den första posten visade vi beroendet av värdet av en geometrisk progressionsmedlem på dess ordningsnummer, och i den andra posten tog vi helt enkelt värdet av en geometrisk progressionsmedlem för, och ordningsnumret betecknades inte som, utan som. Allt som återstår att göra är att rita grafen.
Låt oss se vad du har. Här är diagrammet jag fick:

Ser? Funktionen minskar, tenderar till noll, men korsar den aldrig, så den minskar oändligt. Låt oss markera våra punkter på grafen, och samtidigt vad koordinaten och betyder:

Försök att schematiskt avbilda en graf över en geometrisk progression om dess första term också är lika. Analysera vad som är skillnaden mot vårt tidigare diagram?
Klarade du dig? Här är diagrammet jag fick:

Nu när du till fullo har förstått grunderna i ämnet geometrisk progression: du vet vad det är, du vet hur du hittar dess term, och du vet också vad en oändligt minskande geometrisk progression är, låt oss gå vidare till dess huvudsakliga egenskap.
egenskapen hos en geometrisk progression.
Kommer du ihåg egenskapen hos medlemmarna i en aritmetisk progression? Ja, ja, hur man hittar värdet av ett visst antal av en progression när det finns tidigare och efterföljande värden för medlemmarna i denna progression. Minns du? Detta:
Nu står vi inför exakt samma fråga för termerna för en geometrisk progression. För att härleda en sådan formel, låt oss börja rita och resonera. Du ska se, det är väldigt enkelt, och om du glömmer det kan du ta fram det själv.
Låt oss ta en annan enkel geometrisk progression, där vi vet och. Hur man hittar? Med en aritmetisk progression är detta enkelt och enkelt, men hur är det här? Faktum är att det inte är något komplicerat i geometri heller - du behöver bara måla varje värde som ges till oss enligt formeln.
Du frågar, och vad ska vi göra med det nu? Ja, väldigt enkelt. Till att börja med, låt oss avbilda dessa formler i figuren och försöka göra olika manipulationer med dem för att komma till ett värde.
Vi abstraherar från de siffror som vi får, vi kommer bara att fokusera på deras uttryck genom en formel. Vi måste hitta värdet markerat i orange, med kunskap om termerna intill det. Låt oss försöka utföra olika åtgärder med dem, som ett resultat av vilka vi kan få.
Tillägg.
Låt oss försöka lägga till två uttryck och vi får:
Från detta uttryck, som du kan se, kommer vi inte att kunna uttrycka på något sätt, därför kommer vi att försöka ett annat alternativ - subtraktion.
Subtraktion.
Som du kan se kan vi inte heller uttrycka från detta, därför kommer vi att försöka multiplicera dessa uttryck med varandra.
Multiplikation.
Titta nu noga på vad vi har, multiplicera termerna för en geometrisk progression som ges till oss i jämförelse med vad som behöver hittas:
Gissa vad jag pratar om? Okej, för att hitta måste vi ta Roten ur från de geometriska progressionstalen som gränsar till det önskade talet multiplicerat med varandra:
Här har du. Du härledde själv egenskapen till en geometrisk progression. Försök att skriva denna formel i allmän form. Hände?
Glömt skick när? Fundera på varför det är viktigt, försök till exempel räkna ut det själv, kl. Vad händer i det här fallet? Det stämmer, fullständigt nonsens, eftersom formeln ser ut så här:
Glöm därför inte denna begränsning.
Låt oss nu beräkna vad som är
Rätt svar - ! Om du inte glömde det andra möjliga värdet när du beräknade, då är du en fantastisk kille och du kan omedelbart gå vidare till träningen, och om du glömde, läs vad som analyseras nedan och var uppmärksam på varför båda rötterna måste skrivas i svaret .
Låt oss rita båda våra geometriska progressioner - den ena med ett värde och den andra med ett värde, och kontrollera om båda har rätt att existera:

För att kontrollera om en sådan geometrisk progression existerar eller inte, är det nödvändigt att se om det är lika mellan alla dess givna medlemmar? Beräkna q för det första och andra fallet.
Förstår du varför vi måste skriva två svar? Eftersom tecknet för den obligatoriska termen beror på om den är positiv eller negativ! Och eftersom vi inte vet vad det är måste vi skriva båda svaren med plus och minus.
Nu när du har bemästrat huvudpunkterna och härlett formeln för egenskapen för en geometrisk progression, hitta, veta och
Jämför dina svar med de rätta:
Vad tror du, tänk om vi inte fick värdena för medlemmarna i den geometriska progressionen som gränsar till det önskade numret, utan på samma avstånd från det. Till exempel måste vi hitta, och ges och. Kan vi använda formeln vi härledde i det här fallet? Försök att bekräfta eller motbevisa denna möjlighet på samma sätt, och beskriv vad varje värde består av, som du gjorde när du härledde formeln initialt, med.
Vad fick du?
Titta nu noga igen.
och motsvarande:
Av detta kan vi dra slutsatsen att formeln fungerar inte bara med angränsande med de önskade termerna för en geometrisk progression, men också med lika långt från vad medlemmarna letar efter.
Således blir vår ursprungliga formel:
Det vill säga, om vi i det första fallet sa det, nu säger vi att det kan vara lika med vilket naturligt tal som helst som är mindre. Huvudsaken är att vara samma för båda givna siffrorna.
Öva på specifika exempel, var bara extremt försiktig!
- , . Hitta.
- , . Hitta.
- , . Hitta.
Bestämt? Jag hoppas att du var extremt uppmärksam och märkte en liten hake.
Vi jämför resultaten.
I de två första fallen tillämpar vi lugnt ovanstående formel och får följande värden:
I det tredje fallet, efter noggrann övervägande av serienumren för de numren som vi fått, förstår vi att de inte är på samma avstånd från numret vi letar efter: det är det tidigare numret, men borttaget på plats, så det är inte möjligt att tillämpa formeln.
Hur löser man det? Det är faktiskt inte så svårt som det verkar! Låt oss skriva ner med dig vad varje nummer som ges till oss och det önskade antalet består av.
Så vi har och. Låt oss se vad vi kan göra med dem. Jag föreslår att dela. Vi får:
Vi ersätter vår data med formeln:
Nästa steg kan vi hitta - för detta måste vi ta kubroten av det resulterande talet.
Låt oss nu titta igen på vad vi har. Vi har, men vi måste hitta, och det är i sin tur lika med:
Vi hittade all nödvändig data för beräkningen. Ersätt i formeln:
Vårt svar: .
Försök att lösa ett annat problem själv:
Givet: ,
Hitta:
Hur mycket fick du? Jag har - .
Som du kan se behöver du faktiskt kom ihåg bara en formel- . Allt resten kan du själv när som helst ta ut utan problem. För att göra detta, skriv helt enkelt den enklaste geometriska progressionen på ett papper och skriv ner vad, enligt ovanstående formel, vart och ett av dess nummer är lika med.
Summan av termerna för en geometrisk progression.
Tänk nu på formlerna som gör att vi snabbt kan beräkna summan av termerna för en geometrisk progression i ett givet intervall:
För att härleda formeln för summan av termer av en ändlig geometrisk progression multiplicerar vi alla delar av ekvationen ovan med. Vi får:
Titta noga: vad har de två sista formlerna gemensamt? Just det, vanliga medlemmar, till exempel och så vidare, förutom den första och sista medlemmen. Låt oss försöka subtrahera den 1:a ekvationen från den 2:a ekvationen. Vad fick du?
Uttryck nu genom formeln för en medlem av en geometrisk progression och ersätt det resulterande uttrycket i vår senaste formel:
Gruppera uttrycket. Du bör få:
Allt som återstår att göra är att uttrycka:
Följaktligen i detta fall.
Tänk om? Vilken formel fungerar då? Föreställ dig en geometrisk progression vid. Hur är hon? Korrekt en serie med identiska siffror, respektive, formeln kommer att se ut så här:
Liksom med aritmetisk och geometrisk progression finns det många legender. En av dem är legenden om Seth, schackets skapare.
Många vet att schackspelet uppfanns i Indien. När den hinduiska kungen träffade henne var han förtjust över hennes kvickhet och de olika positioner som var möjliga i henne. När kungen fick veta att det uppfanns av en av hans undersåtar, bestämde sig kungen för att belöna honom personligen. Han kallade uppfinnaren till sig och beordrade att be honom om vad han ville, och lovade att uppfylla även den mest skickliga önskan.
Seta bad om betänketid, och när Seta nästa dag dök upp inför kungen, överraskade han kungen med den oöverträffade blygsamheten i hans begäran. Han bad om ett vetekorn för den första rutten på schackbrädet, vete för den andra, för den tredje, för den fjärde, och så vidare.
Kungen blev arg och drev Seth iväg och sade att tjänarens begäran var ovärdig kunglig generositet, men lovade att tjänaren skulle få sina korn för alla celler i tavlan.
Och nu är frågan: med hjälp av formeln för summan av medlemmarna i en geometrisk progression, beräkna hur många korn Seth ska få?
Låt oss börja diskutera. Eftersom Seth, enligt villkoret, bad om ett vetekorn för den första cellen på schackbrädet, för den andra, för den tredje, för den fjärde, etc., ser vi att problemet handlar om en geometrisk progression. Vad är lika i det här fallet?
Höger.
Totalt antal celler på schackbrädet. Respektive. Vi har all data, det återstår bara att byta in i formeln och beräkna.
För att representera åtminstone ungefär "skalorna" för ett givet tal, transformerar vi med hjälp av gradens egenskaper:
Naturligtvis, om du vill kan du ta en miniräknare och räkna ut vilken typ av tal du hamnar på, och om inte får du ta mitt ord för det: det slutliga värdet på uttrycket blir.
Det är:
quintillions quadrillion biljoner miljarder miljoner tusen.
Fuh) Om du vill föreställa dig hur enormt detta antal är, uppskatta då vilken storlek ladugård som skulle behövas för att rymma hela spannmålsmängden.
Med en ladugårdshöjd på m och en bredd på m skulle dess längd behöva sträcka sig till km, d.v.s. dubbelt så långt som från jorden till solen.
Om kungen var stark i matematik skulle han kunna erbjuda vetenskapsmannen själv att räkna kornen, för för att räkna en miljon korn skulle han behöva minst en dags outtröttlig räkning, och med tanke på att det är nödvändigt att räkna kvintiljonerna, kornen skulle behöva räknas hela hans liv.
Och nu ska vi lösa ett enkelt problem på summan av termer av en geometrisk progression.
Vasya, en elev i 5:e klass, blev sjuk i influensa, men fortsätter att gå i skolan. Varje dag smittar Vasya två personer som i sin tur infekterar ytterligare två personer, och så vidare. Bara en person i klassen. Om hur många dagar kommer hela klassen att få influensa?
Så den första medlemmen i en geometrisk progression är Vasya, det vill säga en person. medlemmen av den geometriska progressionen, dessa är de två personer som han infekterade den första dagen efter sin ankomst. Den totala summan av medlemmarna i progressionen är lika med antalet elever 5A. Följaktligen talar vi om en utveckling där:
Låt oss ersätta våra data med formeln för summan av termerna för en geometrisk progression:
Hela klassen kommer att bli sjuk inom några dagar. Tror du inte på formler och siffror? Försök själv skildra elevernas "infektion". Hände? Se hur det ser ut för mig:

Räkna själv ut hur många dagar eleverna skulle få influensa om alla skulle smitta en person, och det fanns en person i klassen.
Vilket värde fick du? Det visade sig att alla började bli sjuka efter en dag.
Som du kan se liknar en sådan uppgift och ritningen för den en pyramid, där varje efterföljande "tar" nya människor. Men förr eller senare kommer ett ögonblick då den senare inte kan locka någon. I vårt fall, om vi föreställer oss att klassen är isolerad, sluter personen från kedjan (). Således, om en person var inblandad i en finansiell pyramid där pengar gavs om du tar med två andra deltagare, då personen (eller i allmänt fall) inte skulle ta med någon, respektive skulle förlora allt som de investerat i denna finansiella bluff.
Allt som sades ovan hänvisar till en minskande eller ökande geometrisk progression, men som ni minns har vi en speciell sort - en oändligt minskande geometrisk progression. Hur beräknar man summan av dess medlemmar? Och varför har denna typ av progression vissa funktioner? Låt oss ta reda på det tillsammans.
Så, till att börja med, låt oss titta igen på den här bilden av en oändligt minskande geometrisk progression från vårt exempel:

Och låt oss nu titta på formeln för summan av en geometrisk progression, härledd lite tidigare:
eller
Vad strävar vi efter? Det stämmer, grafen visar att den tenderar mot noll. Det vill säga när, det blir nästan lika, respektive vid beräkning av uttrycket får vi nästan. I detta avseende tror vi att när man beräknar summan av en oändligt minskande geometrisk progression, kan denna konsol försummas, eftersom den kommer att vara lika.
- formeln är summan av termerna för en oändligt minskande geometrisk progression.
VIKTIG! Vi använder formeln för summan av termer av en oändligt minskande geometrisk progression endast om villkoret uttryckligen säger att vi behöver hitta summan ändlös antalet medlemmar.
Om ett specifikt tal n anges använder vi formeln för summan av n termer, även om eller.
Och nu ska vi öva.
- Hitta summan av de första termerna i en geometrisk progression med och.
- Hitta summan av termerna för en oändligt minskande geometrisk progression med och.
Jag hoppas att du var väldigt försiktig. Jämför våra svar:
Nu vet du allt om geometrisk progression, och det är dags att gå från teori till praktik. De vanligaste exponentiella problemen som hittas på provet är problem med ränta. Det är om dem vi ska prata.
Problem med att beräkna sammansatt ränta.
Du måste ha hört talas om den så kallade sammansatta ränteformeln. Förstår du vad hon menar? Om inte, låt oss ta reda på det, för efter att ha insett själva processen kommer du omedelbart att förstå vad den geometriska utvecklingen har med det att göra.
Vi går alla till banken och vet att det finns olika förutsättningar på insättningar: detta är en term, och ytterligare underhåll och ränta med två olika sätt att beräkna det - enkelt och komplext.
MED enkel ränta allt är mer eller mindre klart: ränta debiteras en gång vid slutet av insättningsperioden. Det vill säga, om vi pratar om att lägga 100 rubel per år under, kommer de att krediteras först i slutet av året. Följaktligen kommer vi att få rubel i slutet av insättningen.
Ränta på räntaär ett alternativ där räntekapitalisering, dvs. deras tillägg till beloppet av insättningen och den efterföljande beräkningen av inkomsten inte från den ursprungliga, utan från det ackumulerade beloppet av insättningen. Kapitalisering sker inte konstant, men med viss periodicitet. I regel är sådana perioder lika och oftast använder bankerna en månad, ett kvartal eller ett år.
Låt oss säga att vi sätter alla samma rubel per år, men med en månatlig kapitalisering av insättningen. Vad får vi?
Förstår du allt här? Om inte, låt oss ta det steg för steg.
Vi tog med rubel till banken. I slutet av månaden bör vi ha ett belopp på vårt konto bestående av våra rubel plus ränta på dem, det vill säga:
Hålla med?
Vi kan ta ut det ur fästet och då får vi:
Håller med, den här formeln är redan mer lik den vi skrev i början. Det återstår att ta itu med procentsatser
I problemets tillstånd får vi veta om det årliga. Som ni vet multiplicerar vi inte med - vi omvandlar procenttal till decimaler, det vill säga:
Höger? Nu frågar du, var kom numret ifrån? Väldigt enkelt!
Jag upprepar: problemets tillstånd säger om ÅRLIG upplupen ränta EN GÅNG I MÅNADEN. Som ni vet kommer banken under ett år av månader att debitera oss en del av den årliga räntan per månad:
Insett? Försök nu att skriva hur denna del av formeln skulle se ut om jag sa att räntan beräknas dagligen.
Klarade du dig? Låt oss jämföra resultaten:

Bra gjort! Låt oss återgå till vår uppgift: skriv ner hur mycket som kommer att krediteras vårt konto för den andra månaden, med hänsyn till att ränta debiteras på det ackumulerade insättningsbeloppet.
Här är vad som hände mig:
Eller med andra ord:

Jag tror att du redan har lagt märke till ett mönster och sett en geometrisk progression i allt detta. Skriv vad dess medlem kommer att vara lika med, eller, med andra ord, hur mycket pengar vi kommer att få i slutet av månaden.
Gjorde det? Kontroll!
Som du kan se, om du lägger pengar på en bank i ett år till en enkel ränta, kommer du att få rubel, och om du sätter dem till en sammansatt ränta får du rubel. Fördelen är liten, men detta händer bara under det e året, men under en längre period är kapitalisering mycket mer lönsamt:

Överväg en annan typ av problem med sammansatt ränta. Efter vad du räknat ut kommer det att vara elementärt för dig. Så uppgiften är:
Zvezda började investera i branschen år 2000 med ett dollarkapital. Varje år sedan 2001 har den gjort en vinst som är lika med föregående års kapital. Hur stor vinst kommer Zvezda-företaget att få i slutet av 2003 om vinsten inte togs ur omlopp?
Huvudstaden i Zvezda-företaget 2000.
- Zvezdas huvudstad 2001.
- Zvezdas huvudstad 2002.
- Zvezdas huvudstad 2003.
Eller så kan vi skriva kort:
För vårt fall:
2000, 2001, 2002 och 2003.
Respektive:
rubel
Observera att vi i denna uppgift inte har en division vare sig med eller med, eftersom procentsatsen anges ÅRLIGT och beräknas ÅRLIGT. Det vill säga när du läser problemet för sammansatt ränta, var uppmärksam på vilken procentsats som ges och under vilken period den debiteras, och fortsätt först sedan till beräkningarna.
Nu vet du allt om geometrisk progression.
Träning.
- Hitta en term för en geometrisk progression om det är känt att, och
- Hitta summan av de första termerna i en geometrisk progression, om det är känt att, och
- MDM Capital började investera i branschen 2003 med ett dollarkapital. Varje år sedan 2004 har hon gjort en vinst som är lika med föregående års kapital. Företaget "MSK Cash Flows" började investera i branschen 2005 till ett belopp av 10 000 $, och började gå med vinst 2006 i mängden. Med hur många dollar överstiger ett företags kapital det i ett annat i slutet av 2007, om vinster inte togs ur cirkulationen?
Svar:
- Eftersom problemets tillstånd inte säger att progressionen är oändlig och det krävs för att hitta summan av ett specifikt antal av dess medlemmar, utförs beräkningen enligt formeln:
Företag "MDM Capital":2003, 2004, 2005, 2006, 2007.
- ökar med 100%, det vill säga 2 gånger.
Respektive:
rubel
MSK kassaflöden:2005, 2006, 2007.
- ökar med, det vill säga gånger.
Respektive:
rubel
rubel
Låt oss sammanfatta.
1) En geometrisk progression ( ) är en numerisk sekvens, vars första term skiljer sig från noll, och varje term, med början från den andra, är lika med den föregående, multiplicerad med samma tal. Detta tal kallas nämnaren för en geometrisk progression.
2) Ekvationen för medlemmarna i en geometrisk progression -.
3) kan ta vilket värde som helst, förutom och.
- om, då har alla efterföljande medlemmar av progressionen samma tecken - de positiv;
- om, då alla efterföljande medlemmar av progressionen alternativa tecken;
- at - progressionen kallas oändligt avtagande.
4) , at är en egenskap för en geometrisk progression (angränsande termer)
eller
, vid (lika avstånd)
När du hittar det, glöm inte det det borde finnas två svar..
Till exempel,
5) Summan av medlemmarna i en geometrisk progression beräknas med formeln:
eller
eller
VIKTIG! Vi använder formeln för summan av termer av en oändligt minskande geometrisk progression endast om villkoret uttryckligen säger att vi behöver hitta summan av ett oändligt antal termer.
6) Uppgifter för sammansatt ränta beräknas också enligt formeln för den e medlemmen i en geometrisk progression, förutsatt att medlen inte tagits ur cirkulation:
GEOMETRISK PROGRESSION. KORT OM HUVUDSAKTEN
Geometrisk progression( ) är en numerisk sekvens, vars första term skiljer sig från noll, och varje term, med början från den andra, är lika med den föregående, multiplicerad med samma tal. Detta nummer kallas nämnaren för en geometrisk progression.
Nämnare för en geometrisk progression kan ta vilket värde som helst förutom och.
- Om alla efterföljande medlemmar av progressionen har samma tecken - de är positiva;
- om då alla efterföljande medlemmar av progressionen växlar tecken;
- at - progressionen kallas oändligt avtagande.
Ekvation för medlemmar av en geometrisk progression - .
Summan av termerna för en geometrisk progression beräknas med formeln:
eller
Om progressionen minskar oändligt, då:
DE ÅTERSTÅENDE 2/3 ARTIKLAR ÄR ENDAST TILLGÄNGLIGA FÖR DINA STUDENTER!
Bli student hos YouClever,
Förbered dig för OGE eller USE i matematik till priset av "en kopp kaffe per månad",
Och få även obegränsad tillgång till läroboken "YouClever", träningsprogrammet "100gia" (lösningsbok), obegränsad provanvändning och OGE, 6000 uppgifter med analys av lösningar och andra YouClever- och 100gia-tjänster.
Formeln för den n:e medlemmen av en geometrisk progression är en mycket enkel sak. Både i betydelse och generellt. Men det finns alla möjliga problem för formeln för den n:e medlemmen - från mycket primitiva till ganska allvarliga. Och i processen för vår bekantskap kommer vi definitivt att överväga dem båda. Nåväl, låt oss träffas?)
Så till att börja med faktiskt formeln
Här är hon:
b n = b 1 · q n -1
Formel som formel, inget övernaturligt. Det ser ännu enklare och mer kompakt ut än den liknande formeln för . Innebörden av formeln är också enkel, som en filtstövel.
Denna formel låter dig hitta ALLA medlem i en geometrisk progression EFTER DESS NUMMER " n".
Som du kan se är betydelsen en fullständig analogi med en aritmetisk progression. Vi känner till talet n - vi kan även räkna ut termen under detta tal. Vad vi vill. Inte multiplicera sekventiellt med "q" många, många gånger. Det är hela poängen.)
Jag förstår att på denna nivå av arbete med progressioner borde alla kvantiteter som ingår i formeln redan vara tydliga för dig, men jag anser att det är min plikt att dechiffrera var och en. För säkerhets skull.
Låt oss gå:
b 1 – först medlem av en geometrisk progression;
q – ;
n- medlemsnummer;
b n – n:a (nth) medlem av en geometrisk progression.
Denna formel kopplar samman de fyra huvudparametrarna för varje geometrisk progression - bn, b 1 , q Och n. Och kring dessa fyra nyckelfigurer kretsar allt-alla uppgifter på gång.
"Och hur visas det?"- Jag hör en nyfiken fråga ... Elementärt! Se!
Vad är lika med andra progressionsmedlem? Inga problem! Vi skriver direkt:
b 2 = b 1 q
Och den tredje medlemmen? Inte ett problem heller! Vi multiplicerar den andra termen igen påq.
Så här:
B 3 \u003d b 2 q
Kom ihåg att den andra termen i sin tur är lika med b 1 q och ersätt detta uttryck med vår likhet:
B 3 = b 2 q = (b 1 q) q = b 1 q q = b 1 q 2
Vi får:
B 3 = b 1 q 2
Låt oss nu läsa vårt inlägg på ryska: tredje term är lika med den första termen multiplicerad med q in andra grad. Förstår du? Inte än? Okej, ett steg till.
Vad är den fjärde termen? Alla likadana! Multiplicera tidigare(dvs den tredje termen) på q:
B 4 \u003d b 3 q \u003d (b 1 q 2) q \u003d b 1 q 2 q \u003d b 1 q 3
Total:
B 4 = b 1 q 3
Och återigen översätter vi till ryska: fjärde term är lika med den första termen multiplicerad med q in tredje grad.
Och så vidare. Så hur är det? Har du fångat mönstret? Ja! För alla termer med valfritt tal kommer antalet lika faktorer q (dvs. nämnarens potens) alltid att vara en mindre än numret på den önskade medlemmenn.
Därför kommer vår formel att vara, utan alternativ:
bn =b 1 · q n -1
Det är allt.)
Tja, låt oss lösa problem, ska vi?)
Lösa problem på en formelntermen av en geometrisk progression.
Låt oss börja, som vanligt, med en direkt tillämpning av formeln. Här är ett typiskt problem:
Det är känt exponentiellt b 1 = 512 och q = -1/2. Hitta den tionde termen i progressionen.
Naturligtvis kan detta problem lösas utan några formler alls. Precis som en geometrisk progression. Men vi måste värma upp med formeln för den n:e termen, eller hur? Här bryter vi upp.
Våra data för att tillämpa formeln är följande.
Den första termen är känd. Det här är 512.
b 1 = 512.
Nämnaren för progressionen är också känd: q = -1/2.
Det återstår bara att ta reda på vad numret på termen n är lika med. Inga problem! Är vi intresserade av den tionde terminen? Så vi ersätter tio istället för n i den allmänna formeln.
Och beräkna noggrant aritmetiken:
Svar: -1
Som du kan se visade sig den tionde terminen av progressionen vara med ett minus. Inte konstigt: nämnaren för progressionen är -1/2, d.v.s. negativ siffra. Och detta säger oss att tecknen på vår utveckling växlar, ja.)
Allt är enkelt här. Och här är ett liknande problem, men lite mer komplicerat när det gäller beräkningar.
I geometrisk progression vet vi att:
b 1 = 3
Hitta den trettonde termen i progressionen.
Allt är sig likt, bara den här gången är nämnaren för progressionen - irrationell. Roten av två. Nåväl, ingen stor sak. Formeln är en universell sak, den klarar alla siffror.
Vi arbetar direkt enligt formeln:
Formeln fungerade så klart som den skulle, men ... det är här några kommer att hänga. Vad ska man göra sedan med roten? Hur höjer man en rot till tolfte makten?
Hur-hur ... Du måste förstå att vilken formel som helst, naturligtvis, är bra, men kunskapen om all tidigare matematik upphävs inte! Hur höjer man? Ja, kom ihåg gradernas egenskaper! Låt oss ändra roten till bråkdelgrad och - genom formeln att höja en makt till en makt.
Så här:
Svar: 192
Och alla saker.)
Vad är den största svårigheten med direkt tillämpning av den n:e termformeln? Ja! Den största svårigheten är jobba med examina! Nämligen exponentiering negativa tal, fraktioner, rötter och liknande strukturer. Så de som har problem med detta, en brådskande begäran att upprepa graderna och deras egenskaper! Annars kommer du sakta ner i det här ämnet, ja ...)
Låt oss nu lösa typiska sökproblem ett av delarna i formeln om alla andra ges. För en framgångsrik lösning av sådana problem är receptet enkelt och enkelt att skrämma - skriv formelnnmedlem i allmänhet! Precis i anteckningsboken bredvid skicket. Och sedan, utifrån tillståndet, räknar vi ut vad som ges till oss och vad som inte räcker. Och vi uttrycker det önskade värdet från formeln. Allt!
Till exempel ett sådant ofarligt problem.
Den femte termen i en geometrisk progression med nämnaren 3 är 567. Hitta den första termen i denna progression.
Inget komplicerat. Vi arbetar direkt enligt besvärjelsen.
Vi skriver formeln för den n:e termen!
b n = b 1 · q n -1
Vad ges till oss? Först ges nämnaren för progressionen: q = 3.
Dessutom är vi givna femte terminen: b 5 = 567 .
Allt? Nej! Vi får också numret n! Detta är en femma: n = 5.
Jag hoppas att du redan förstår vad som står i protokollet b 5 = 567 två parametrar är dolda på en gång - detta är den femte medlemmen själv (567) och dess nummer (5). I en liknande lektion på har jag redan pratat om detta, men jag tror att det inte är överflödigt att påminna här.)
Nu ersätter vi våra data med formeln:
567 = b 1 3 5-1
Vi överväger aritmetik, förenklar och får en enkel linjär ekvation:
81 b 1 = 567
Vi löser och får:
b 1 = 7
Som du kan se är det inga problem med att hitta den första medlemmen. Men när man letar efter nämnaren q och siffror n det kan finnas överraskningar. Och du måste också vara beredd på dem (överraskningar), ja.)
Till exempel ett sådant problem:
Den femte termen i en geometrisk progression med en positiv nämnare är 162, och den första termen i denna progression är 2. Hitta progressionens nämnare.
Den här gången får vi den första och den femte medlemmen och ombeds hitta nämnaren för progressionen. Här börjar vi.
Vi skriver formelnnmedlem!
b n = b 1 · q n -1
Våra initiala uppgifter kommer att vara följande:
b 5 = 162
b 1 = 2
n = 5
Inte tillräckligt värde q. Inga problem! Låt oss hitta det nu.) Vi ersätter allt vi vet i formeln.
Vi får:
162 = 2q 5-1
2 q 4 = 162
q 4 = 81
En enkel ekvation av fjärde graden. Men nu - försiktigt! I detta skede av lösningen extraherar många studenter omedelbart med glädje roten (av fjärde graden) och får svaret q=3 .
Så här:
q4 = 81
q = 3
Men generellt sett är detta ett oavslutat svar. Eller snarare ofullständig. Varför? Poängen är att svaret q = -3 passar också: (-3) 4 skulle också vara 81!
Allt för att effektekvation x n = a alltid har två motsatta rötter på ävenn . Plus och minus:
Båda passar.
Till exempel att lösa (dvs. andra grader)
x2 = 9
Av någon anledning är du inte förvånad över utseendet två rötter x=±3? Det är samma sak här. Och med någon annan även grad (fjärde, sjätte, tionde, etc.) kommer att vara densamma. Detaljer - i ämnet om
Det är därför rätt lösning kommer att bli så här:
q 4 = 81
q= ±3
Okej, vi har reda ut tecknen. Vilken är rätt - plus eller minus? Tja, vi läser tillståndet för problemet igen på jakt efter ytterligare information. Det kan naturligtvis inte existera, men i detta problem sådan information tillgängliga. I vårt tillstånd står det direkt att en progression ges med positiv nämnare.
Så svaret är uppenbart:
q = 3
Allt är enkelt här. Vad tror du skulle hända om problemformuleringen var så här:
Den femte termen i en geometrisk progression är 162, och den första termen i denna progression är 2. Hitta progressionens nämnare.
Vad är skillnaden? Ja! I skicket Ingenting inget omnämnande av nämnaren. Varken direkt eller indirekt. Och här skulle problemet redan ha två lösningar!
q = 3 Och q = -3
Jaja! Och med plus och minus.) Matematiskt skulle detta faktum innebära att det finns två förlopp som passar uppgiften. Och för var och en - sin egen nämnare. För skojs skull, öva och skriv ner de första fem termerna av varje.)
Låt oss nu öva på att hitta medlemsnumret. Det här är det svåraste, ja. Men också mer kreativ.
Givet en geometrisk progression:
3; 6; 12; 24; …
Vilket nummer är 768 i denna utveckling?
Det första steget är detsamma: skriv formelnnmedlem!
b n = b 1 · q n -1
Och nu, som vanligt, ersätter vi de uppgifter som vi känner till i den. Hm... det passar inte! Var är den första medlemmen, var är nämnaren, var är allt annat?!
Var, var ... Varför behöver vi ögon? Flappande ögonfransar? Denna gång ges progressen till oss direkt i formuläret sekvenser. Kan vi se den första termen? Vi ser! Detta är en trippel (b 1 = 3). Hur är det med nämnaren? Vi ser det inte än, men det är väldigt lätt att räkna. Om du förstår förstås.
Här överväger vi. Direkt enligt betydelsen av en geometrisk progression: vi tar någon av dess medlemmar (förutom den första) och dividerar med den föregående.
Åtminstone så här:
q = 24/12 = 2
Vad vet vi mer? Vi känner också till någon medlem av denna progression, lika med 768. Under något nummer n:
b n = 768
Vi vet inte hans nummer, men vår uppgift är just att hitta honom.) Så vi letar efter. Vi har redan laddat ner all nödvändig data för substitution i formeln. Omärkligt.)
Här ersätter vi:
768 = 3 2n -1
Vi gör elementära - vi delar båda delarna med tre och skriver om ekvationen i den vanliga formen: det okända till vänster, det kända till höger.
Vi får:
2 n -1 = 256
Här är en intressant ekvation. Vi måste hitta "n". Vad är ovanligt? Ja, jag argumenterar inte. Egentligen är det det enklaste. Det kallas så för att det okända (i det här fallet är det numret n) står i indikator grad.
Vid bekantskapsstadiet med en geometrisk progression (detta är nionde klass) exponentiella ekvationer de lär dig inte att bestämma, ja ... Detta är ämnet för seniorklasserna. Men det finns inget hemskt. Även om du inte vet hur sådana ekvationer löses, låt oss försöka hitta vår n vägleds av enkel logik och sunt förnuft.
Vi börjar diskutera. Till vänster har vi en tvåa till en viss grad. Vi vet ännu inte exakt vad den här graden är, men det här är inte skrämmande. Men å andra sidan vet vi bestämt att denna grad är lika med 256! Så vi kommer ihåg i vilken utsträckning tvåan ger oss 256. Kommer du ihåg? Ja! I åttonde grader!
256 = 2 8
Om du inte kom ihåg eller med erkännandet av graden av problemet, så är det också okej: vi höjer bara de två sekventiellt till kvadraten, till kuben, till fjärde potensen, den femte, och så vidare. Urvalet, faktiskt, men på den här nivån, är en riktig åktur.
På ett eller annat sätt får vi:
2 n -1 = 2 8
n-1 = 8
n = 9
Så 768 är nionde medlem av vår progression. Det var allt, problemet löst.)
Svar: 9
Vad? Tråkig? Trött på det elementära? Hålla med. Och jag också. Låt oss gå till nästa nivå.)
Mer komplexa uppgifter.
Och nu löser vi pusslen mer abrupt. Inte direkt supercool, men som man måste jobba lite på för att komma fram till svaret.
Till exempel så här.
Hitta den andra termen i en geometrisk progression om dess fjärde term är -24 och den sjunde termen är 192.
Detta är en klassiker i genren. Några två olika medlemmar av progressionen är kända, men ytterligare en medlem måste hittas. Dessutom är alla medlemmar INTE grannar. Vad förvirrar först, ja...
Som i överväger vi två metoder för att lösa sådana problem. Det första sättet är universellt. Algebraisk. Fungerar felfritt med alla källdata. Så det är där vi börjar.)
Vi målar varje term enligt formeln nmedlem!
Allt är exakt detsamma som med en aritmetisk progression. Bara den här gången jobbar vi med annan allmän formel. Det är allt.) Men kärnan är densamma: vi tar och i tur och ordning vi ersätter våra initiala data med formeln för den n:e termen. För varje medlem - sin egen.
För fjärde terminen skriver vi:
b 4 = b 1 · q 3
-24 = b 1 · q 3
Äta. En ekvation är klar.
För den sjunde terminen skriver vi:
b 7 = b 1 · q 6
192 = b 1 · q 6
Totalt erhölls två ekvationer för samma progression .
Vi sätter ihop ett system från dem:

Trots sitt formidabla utseende är systemet ganska enkelt. Det mest uppenbara sättet att lösa är den vanliga substitutionen. Vi uttrycker b 1 från den övre ekvationen och ersätt med den nedre:

Lite pyssel med den lägre ekvationen (minska exponenterna och dividera med -24) ger:
q 3 = -8
Förresten, samma ekvation kan man komma fram till på ett enklare sätt! Vad? Nu ska jag visa dig ett annat hemligt, men väldigt vackert, kraftfullt och användbart sätt att lösa sådana system. Sådana system, i vars ekvationer de sitter fungerar bara.Åtminstone i en. kallad termindelningsmetod en ekvation till en annan.
Så vi har ett system:
I båda ekvationerna till vänster - arbete, och till höger är bara en siffra. Detta är ett mycket bra tecken.) Låt oss ta och ... dividera, säg, den nedre ekvationen med den övre! Vad betyder, dividera en ekvation med en annan? Väldigt enkelt. Vi tar vänster sida en ekvation (lägre) och vi delar henne på vänster sida en annan ekvation (övre). Den högra sidan är liknande: höger sida en ekvation vi delar på höger sida annan.
Hela uppdelningsprocessen ser ut så här:

När vi nu minskar allt som minskar får vi:
q 3 = -8
Vad är bra med den här metoden? Ja, för i processen med en sådan uppdelning kan allt dåligt och obekvämt säkert reduceras och en helt ofarlig ekvation kvarstår! Det är därför det är så viktigt att ha bara multiplikationer i åtminstone en av systemets ekvationer. Det finns ingen multiplikation - det finns inget att reducera, ja ...
I allmänhet förtjänar denna metod (som många andra icke-triviala sätt att lösa system) till och med en separat lektion. Jag ska definitivt titta närmare på det. Någon dag…
Men oavsett hur du löser systemet, i alla fall måste vi nu lösa den resulterande ekvationen:
q 3 = -8
Inga problem: vi extraherar roten (kubisk) och - klart!
![]()
Observera att det inte är nödvändigt att sätta plus/minus här vid extrahering. Vi har en udda (tredje) grads rot. Och svaret är detsamma, ja.
Så, nämnaren för progression finns. Minus två. Bra! Processen är igång.)
För den första termen (säg från den översta ekvationen) får vi:
![]()
Bra! Vi känner till den första termen, vi känner till nämnaren. Och nu har vi möjlighet att hitta vilken medlem som helst i progressionen. Inklusive den andra.)
För den andra medlemmen är allt ganska enkelt:
b 2 = b 1 · q= 3 (-2) = -6
Svar: -6
Så vi har sorterat ut det algebraiska sättet att lösa problemet. Svår? Inte mycket, jag håller med. Långt och tråkigt? Ja definitivt. Men ibland kan man minska arbetet avsevärt. För detta finns grafiskt sätt. God gammal och bekant för oss av .)
Låt oss rita problemet!
Ja! Exakt. Återigen skildrar vi vår utveckling på talaxeln. Inte nödvändigtvis av en linjal, det är inte nödvändigt att hålla lika intervall mellan medlemmarna (vilket förresten inte kommer att vara detsamma, eftersom progressionen är geometrisk!), utan helt enkelt schematiskt rita vår sekvens.
Jag fick det så här:

Titta nu på bilden och fundera. Hur många lika faktorer "q" delar fjärde Och sjunde medlemmar? Det stämmer, tre!
Därför har vi all rätt att skriva:
-24q 3 = 192
Härifrån är det nu lätt att hitta q:
q 3 = -8
q = -2
Det är bra, nämnaren finns redan i vår ficka. Och nu tittar vi på bilden igen: hur många sådana nämnare sitter mellan andra Och fjärde medlemmar? Två! Därför kommer vi att höja nämnaren för att registrera relationen mellan dessa medlemmar kvadrat.
Här skriver vi:
b 2 · q 2 = -24 , var b 2 = -24/ q 2
Vi ersätter vår hittade nämnare i uttrycket för b 2 , räkna och få:
![]()
Svar: -6
Som du kan se är allt mycket enklare och snabbare än genom systemet. Dessutom, här behövde vi inte ens räkna den första termen alls! Alls.)
Här är ett så enkelt och visuellt vägljus. Men det har också en allvarlig nackdel. gissade? Ja! Det är bara bra för mycket korta bitar av progression. De där avstånden mellan medlemmarna av intresse för oss inte är särskilt stora. Men i alla andra fall är det redan svårt att rita en bild, ja... Då löser vi problemet analytiskt, genom ett system.) Och system är en universell sak. Ta itu med vilket nummer som helst.
Ännu en episk:
Den andra termen i den geometriska progressionen är 10 mer än den första, och den tredje termen är 30 mer än en sekund. Hitta nämnaren för progressionen.
Vad är coolt? Inte alls! Alla likadana. Vi översätter återigen problemets tillstånd till ren algebra.
1) Vi målar varje term enligt formeln nmedlem!
Andra termen: b 2 = b 1 q
Tredje termen: b 3 \u003d b 1 q 2
2) Vi skriver ner relationen mellan medlemmarna utifrån problemets tillstånd.
Läser villkoret: "Den andra termen i en geometrisk progression är 10 mer än den första." Sluta, det här är värdefullt!
Så vi skriver:
b 2 = b 1 +10
Och vi översätter den här frasen till ren matematik:
b 3 = b 2 +30
Vi har två ekvationer. Vi kombinerar dem till ett system:
![]()
Systemet ser enkelt ut. Men det finns många olika index för bokstäver. Låt oss ersätta i stället för den andra och tredje medlemmen av deras uttryck genom den första medlemmen och nämnaren! Förgäves, eller vad, vi målade dem?
Vi får:
![]()
Men ett sådant system är inte längre en gåva, ja ... Hur löser man detta? Tyvärr, den universella hemliga besvärjelsen för att lösa komplex icke-linjär Det finns inga system i matematik och det kan det inte finnas. Det är fantastiskt! Men det första du bör tänka på när du försöker gnaga igenom sådana tuffing- är att gissa Men är inte en av systemets ekvationer reducerad till en vacker form, vilket gör det enkelt att till exempel uttrycka en av variablerna i termer av en annan?
Låt oss gissa. Systemets första ekvation är klart enklare än den andra. Vi kommer att tortera honom.) Varför inte försöka från den första ekvationen något uttrycka genom något? Eftersom vi vill hitta nämnaren q, då vore det mest fördelaktigt för oss att uttrycka b 1 genom q.
Så låt oss försöka göra den här proceduren med den första ekvationen, med de gamla goda:
b1q = b1+10
b 1 q - b 1 \u003d 10
b 1 (q-1) = 10
Allt! Här har vi uttryckt onödig oss variabeln (b 1) genom nödvändig(q). Ja, inte det enklaste uttrycket man fått. Någon slags bråkdel... Men vårt system håller en hyfsad nivå, ja.)
![]()
Typisk. Vad man ska göra - vi vet.
Vi skriver ODZ (Nödvändigtvis!) :
q ≠ 1
Vi multiplicerar allt med nämnaren (q-1) och reducerar alla bråk:
10 q 2 = 10 q + 30(q-1)
Vi delar allt med tio, öppnar fästena, samlar allt till vänster:
q 2 – 4 q + 3 = 0
Vi löser resultatet och får två rötter:
q 1 = 1
q 2 = 3
Det finns bara ett sista svar: q = 3 .
Svar: 3
Som du kan se är sättet att lösa de flesta problem för formeln för den n:te medlemmen av en geometrisk progression alltid detsamma: vi läser uppmärksamt problemets tillstånd och med hjälp av formeln för den n:e termen översätter vi hela användbar information till ren algebra.
Nämligen:
1) Vi skriver separat varje medlem som ges i problemet enligt formelnnmedlemmen.
2) Från problemets tillstånd översätter vi kopplingen mellan medlemmarna till en matematisk form. Vi sammanställer en ekvation eller ett ekvationssystem.
3) Vi löser den resulterande ekvationen eller ekvationssystemet, hittar de okända parametrarna för progressionen.
4) I händelse av ett tvetydigt svar läser vi noggrant problemets tillstånd för att leta efter ytterligare information (om någon). Vi kontrollerar också det mottagna svaret med villkoren för ODZ (om några).
Och nu listar vi huvudproblemen som oftast leder till fel i processen att lösa geometriska progressionsproblem.
1. Elementär aritmetik. Operationer med bråktal och negativa tal.
2. Om åtminstone en av dessa tre punkter är ett problem, kommer du oundvikligen att ha fel i detta ämne. Tyvärr... Så var inte lat och upprepa det som nämndes ovan. Och följ länkarna - gå. Ibland hjälper det.)
Modifierade och återkommande formler.
Och låt oss nu titta på ett par typiska tentamensproblem med en mindre bekant presentation av tillståndet. Ja, ja, du gissade rätt! Detta ändrad Och återkommande formler för den n:e medlemmen. Vi har redan stött på sådana formler och arbetat i aritmetisk progression. Allt är sig likt här. Kärnan är densamma.
Till exempel, ett sådant problem från OGE:
Den geometriska progressionen ges av formeln b n = 3 2 n . Hitta summan av den första och fjärde termen.
Den här gången ges utvecklingen till oss inte riktigt som vanligt. Någon form av formel. Än sen då? Denna formel är också en formelnmedlem! Vi vet alla att formeln för den n:e termen kan skrivas både i allmän form, genom bokstäver och för specifik progression. MED specifik första termen och nämnaren.
I vårt fall får vi faktiskt en generell termformel för en geometrisk progression med följande parametrar:
b 1 = 6
q = 2
Låt oss kolla?) Låt oss skriva formeln för den n:e termen i allmän form och ersätta den i den b 1 Och q. Vi får:
b n = b 1 · q n -1
b n= 6 2n -1
Vi förenklar med hjälp av faktorisering och effektegenskaper och får:
b n= 6 2n -1 = 3 2 2n -1 = 3 2n -1+1 = 3 2n
Som du kan se är allt rättvist. Men vårt mål med dig är inte att visa härledningen av en specifik formel. Detta är sant, lyrisk utvikning. Rent för förståelse.) Vårt mål är att lösa problemet enligt den formel som ges till oss i tillståndet. Får du det?) Så vi arbetar med den modifierade formeln direkt.
Vi räknar första terminen. Ersättning n=1 i den allmänna formeln:
b 1 = 3 2 1 = 3 2 = 6
Så här. Förresten, jag är inte för lat och återigen kommer jag att uppmärksamma er på en typisk blunder med beräkningen av den första termen. Titta INTE på formeln b n= 3 2n, skynda genast att skriva att den första medlemmen är en trojka! Det är ett stort misstag, ja...)
Vi fortsätter. Ersättning n=4 och överväg den fjärde termen:
b 4 = 3 2 4 = 3 16 = 48
Och slutligen beräknar vi det nödvändiga beloppet:
b 1 + b 4 = 6+48 = 54
Svar: 54
Ett annat problem.
Den geometriska progressionen ges av förhållandena:
b 1 = -7;
b n +1 = 3 b n
Hitta den fjärde termen i progressionen.
Här ges progressionen av den återkommande formeln. Tja, okej.) Hur man arbetar med denna formel – det vet vi också.
Här agerar vi. Steg för steg.
1) räkna två på varandra följande medlem av progressionen.
Den första mandatperioden är redan given till oss. Minus sju. Men nästa, andra term, kan enkelt beräknas med den rekursiva formeln. Om du förstår hur det fungerar, förstås.)
Här överväger vi den andra termen enligt den berömda första:
b 2 = 3 b 1 = 3 (-7) = -21
2) Vi överväger nämnaren för progressionen
Inte heller några problem. Rakt, dela andra kuk på först.
Vi får:
q = -21/(-7) = 3
3) Skriv formelnnmedlemmen i vanlig form och överväga den önskade medlemmen.
Så vi känner till den första termen, nämnaren också. Här skriver vi:
b n= -7 3n -1
b 4 = -7 3 3 = -7 27 = -189
Svar: -189
Som du kan se skiljer sig arbetet med sådana formler för en geometrisk progression i huvudsak inte från det för en aritmetisk progression. Det är bara viktigt att förstå den allmänna essensen och innebörden av dessa formler. Nåväl, innebörden av geometrisk progression måste också förstås, ja.) Och då blir det inga dumma misstag.
Tja, låt oss bestämma själva?)
Ganska elementära uppgifter, för uppvärmning:
1. Givet en geometrisk progression där b 1 = 243, och q = -2/3. Hitta den sjätte termen i progressionen.
2. Den gemensamma termen för en geometrisk progression ges av formeln b n = 5∙2 n +1 . Hitta numret på den sista tresiffriga medlemmen i denna progression.
3. Den geometriska progressionen ges av förhållandena:
b 1 = -3;
b n +1 = 6 b n
Hitta den femte termen i progressionen.
Lite mer komplicerat:
4. Givet en geometrisk progression:
b 1 =2048; q =-0,5
Vilken är den sjätte negativa termen i det?
Vad verkar supersvårt? Inte alls. Logik och förståelse för innebörden av geometrisk progression kommer att spara. Jo, formeln för den n:e termen, förstås.
5. Den tredje termen i den geometriska progressionen är -14 och den åttonde termen är 112. Hitta nämnaren för progressionen.
6. Summan av den första och andra termen i en geometrisk progression är 75, och summan av den andra och tredje termen är 150. Hitta den sjätte termen i progressionen.
Svar (i oordning): 6; -3888; -1; 800; -32; 448.
Det är nästan allt. Det återstår bara att lära sig att räkna summan av de första n termerna av en geometrisk progression ja upptäcka oändligt minskande geometrisk progression och dess mängd. En väldigt intressant och ovanlig sak, förresten! Mer om det i senare lektioner.)
Relaterad lektion "Oändligt minskande geometrisk progression"
Syftet med lektionen: introducerar eleverna för en ny typ av sekvens - en oändligt minskande geometrisk progression.
Uppgifter:
formulering av den ursprungliga idén om gränsen för den numeriska sekvensen; bekantskap med ett annat sätt att omvandla oändliga periodiska bråk till vanliga med formeln för summan av en oändligt minskande geometrisk progression;
utveckling av de intellektuella egenskaperna hos skolbarnens personlighet, som t.ex logiskt tänkande, förmåga att bedömningsåtgärder, generalisering;
utbildning av aktivitet, ömsesidig hjälp, kollektivism, intresse för ämnet.
Utrustning: datorklass, projektor, duk.
Lektionstyp: lektion - lärande nytt ämne.
Under lektionerna
jag . Org. ögonblick. Meddelande om ämnet och syftet med lektionen.
II . Uppdatering av elevers kunskaper.1. Kontrollera läxor.
1) Verifiering av grundläggande formler relaterade till aritmetiska och geometriska progressioner. Två elever skriver ner formler vid tavlan.
2) Det gör resten av eleverna matematisk diktering på ämnet "Sumformler".
Uppgifter:
№1. Hitta summan av de första fem medlemmarna av en aritmetisk progression om dess första medlem är 6 (1:a alternativet), -20 (2:a alternativet), och den femte medlemmen är -6 (1:a alternativet), 20 (2:a alternativet).
№2. Hitta summan av de första fem termerna i en aritmetisk progression om dess första term är -20(1:a alternativet), 6(2:a alternativet) och skillnaden är 10(1:a alternativet), -3(2:a alternativet).
№3. Hitta summan av de första fem termerna i en geometrisk progression om dess första term är 1(1:a alternativet), -1 (2:a alternativet), och nämnaren är -2(1:a alternativet), 2(2:a alternativet).
I slutet av diktatet kontrolleras selektivt två elevers arbeten för utvärdering, resten utför självgranskning enligt färdiga lösningar skrivna på tavlans lapels.
Lösningar:

Uppgifter
1. Aritmetisk progression ges av formeln a n = 7 – 4 n. Hitta a 10 . (-33)
2. Aritmetisk progression a 3 = 7 Och a 5 = 1 . Hitta a 4 . (4)
3. Aritmetisk progression a 3 = 7 Och a 5 = 1 . Hitta a 17 . (-35)
4. Aritmetisk progression a 3 = 7 Och a 5 = 1 . Hitta S 17 . (-187)
5. För en geometrisk progression  hitta den femte termen.
hitta den femte termen. 
6. För en geometrisk progression  hitta n-te medlemmen.
hitta n-te medlemmen. 
7. Exponentiellt b 3 = 8 Och b 5 = 2 . Hitta b 4 . (4)
8. Exponentiellt b
3
= 8
Och b
5
= 2
. Hitta b
1
Och
q
. 
9. Exponentiellt b 3 = 8 Och b 5 = 2 . Hitta S 5 . (62)
III . Utforskar ett nytt ämne(demonstration presentation).

Betrakta en ruta med en sida lika med 1. Låt oss rita en annan ruta, vars sida är halva den första kvadraten, sedan en annan, vars sida är halva den andra, sedan nästa, och så vidare. Varje gång är sidan av den nya kvadraten hälften av den föregående.
Som ett resultat fick vi en sekvens av sidor av rutor  bildar en geometrisk progression med nämnare.
bildar en geometrisk progression med nämnare.
Och det som är väldigt viktigt, ju mer vi bygger sådana rutor, desto mindre blir sidan av torget. Till exempel,

De där. när antalet n ökar närmar sig termerna för progressionen noll.
Med hjälp av denna figur kan ytterligare en sekvens övervägas.

Till exempel, sekvensen av områden med kvadrater:

 . Och igen, om nökar på obestämd tid, sedan närmar sig området noll godtyckligt nära.
. Och igen, om nökar på obestämd tid, sedan närmar sig området noll godtyckligt nära.
Låt oss överväga ytterligare ett exempel. En liksidig triangel med en sida på 1 cm. Låt oss bygga nästa triangel med hörn i mittpunkterna på sidorna i den första triangeln, enligt triangelns mittlinjesats - sidan på den andra är lika med halva sidan av den första, sidan på den tredje är halva sidan av 2:an osv. Återigen får vi en sekvens av längder på trianglarnas sidor.
 på
på  .
.
Om vi betraktar en geometrisk progression med en negativ nämnare.
Sedan, igen, med ökande antal n villkoren för progressionen närmar sig noll.
Låt oss vara uppmärksamma på nämnare för dessa sekvenser. Överallt var nämnarna mindre än 1 modulo.
Vi kan dra slutsatsen: en geometrisk progression kommer att minska oändligt om modulen för dess nämnare är mindre än 1.
Framarbete.
Definition:
En geometrisk progression sägs vara oändligt avtagande om modulen för dess nämnare är mindre än en.  .
.
Med hjälp av definitionen är det möjligt att lösa frågan om en geometrisk progression är oändligt avtagande eller inte.
Uppgift
Är sekvensen en oändligt minskande geometrisk progression om den ges av formeln:
 ;
;  .
.
Lösning:
 . Låt oss hitta q
.
. Låt oss hitta q
.
 ;
;  ;
;  ;
;  .
.
denna geometriska progression minskar oändligt.
b) given sekvensär inte en oändligt minskande geometrisk progression.

Betrakta en kvadrat med en sida lika med 1. Dela den på mitten, en av halvorna på mitten igen, och så vidare. områdena för alla resulterande rektanglar bildar en oändligt minskande geometrisk progression: ![]()
Summan av areorna för alla rektanglar som erhålls på detta sätt kommer att vara lika med arean av den första kvadraten och lika med 1. ![]()
Men på vänster sida av denna likhet finns summan av ett oändligt antal termer.
Betrakta summan av de första n termerna. ![]()
Enligt formeln för summan av de första n termerna i en geometrisk progression är den lika med  .
.
Om nökar på obestämd tid alltså
eller  . Det är därför
. Det är därför  , dvs.
, dvs.  .
.
Summan av en oändligt minskande geometrisk progression det finns en sekvensgräns S 1 , S 2 , S 3 , …, S n , … .
Till exempel för en progression  ,
,
 Därför att
Därför att 
Summan av en oändligt minskande geometrisk progression kan hittas med hjälp av formeln 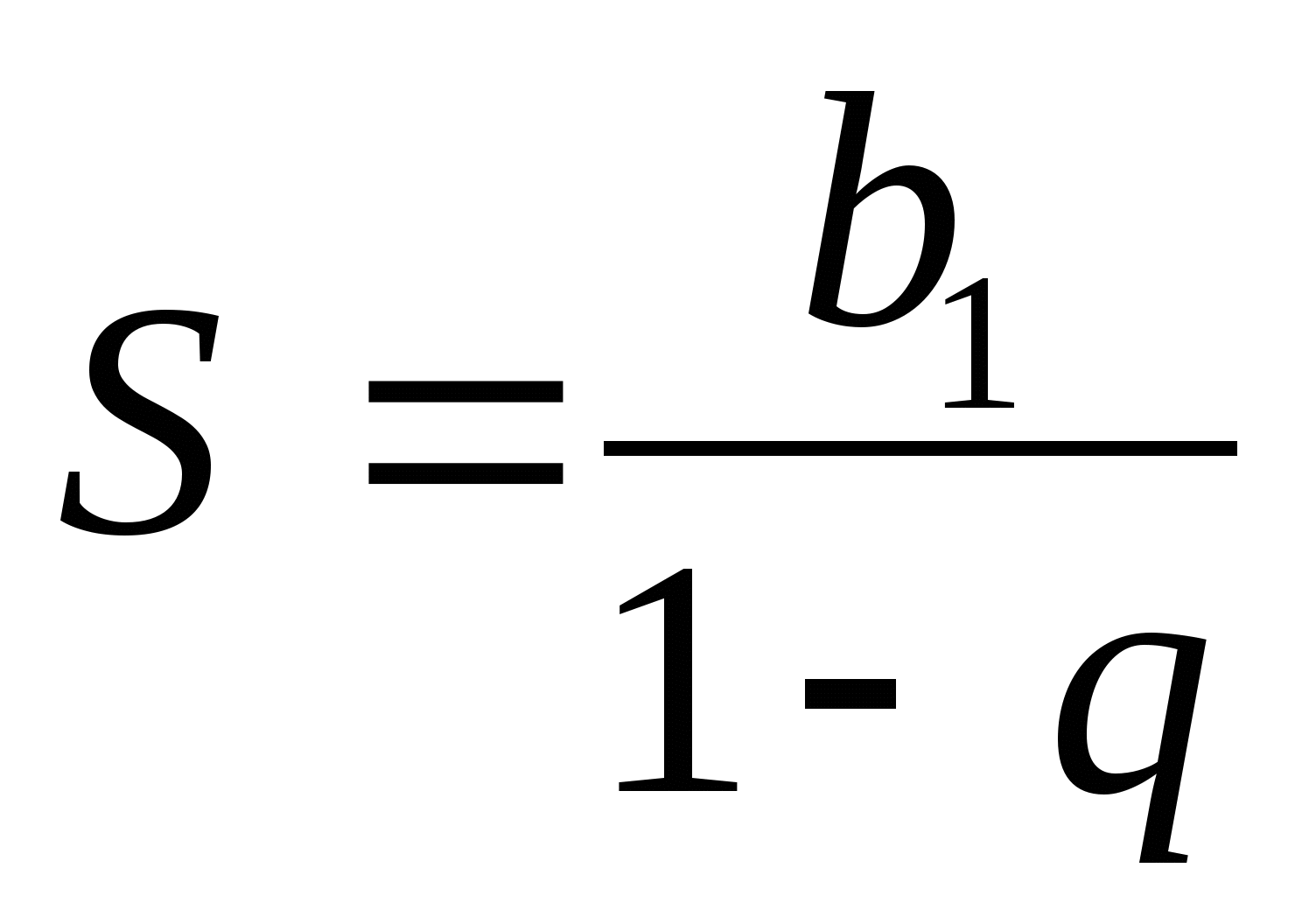 .
.
III . Reflektion och konsolidering(slutförande av uppgifter).
Uppgift nummer 2. Hitta summan av en oändligt minskande geometrisk progression med den första termen 3, den andra 0,3.
Lösning:
Uppgift nummer 3. lärobok, s. 160, nr 433(1)
Hitta summan av en oändligt minskande geometrisk progression:
Lösning:

Uppgift nummer 4. Skriv det oändliga periodiska decimalbråket 0,(5) som ett gemensamt bråktal.
1:a vägen. Låt x = 0, (5) = 0,555 ... / 10 2:a metoden. 0,(5)=0,555…=

Uppgift nummer 5. lärobok, s. 162, nr 445(3) ( oberoende lösning)
Skriv det oändliga periodiska decimalbråket 0,(12) som ett gemensamt bråktal.
Svar: 0,(12)=4/33.
IV . Sammanfattande.
Vilken sekvens mötte du idag?
Definiera en oändligt minskande geometrisk progression.
Hur bevisar man att en geometrisk progression minskar oändligt?
Ge formeln för summan av en oändligt minskande geometrisk progression.
V . Läxa.
En geometrisk progression är en numerisk sekvens, vars första term är icke-noll, och varje nästa term är lika med föregående term multiplicerad med samma icke-nolltal.
Begreppet geometrisk progression
Den geometriska progressionen betecknas med b1,b2,b3, …, bn, … .
Förhållandet mellan en term av det geometriska felet och dess föregående term är lika med samma tal, det vill säga b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Detta följer direkt av definitionen av en aritmetisk progression. Detta tal kallas nämnaren för en geometrisk progression. Vanligtvis betecknas nämnaren för en geometrisk progression med bokstaven q.
Summan av en oändlig geometrisk progression för |q|<1
Ett sätt att ställa in en geometrisk progression är att sätta dess första term b1 och nämnaren för det geometriska felet q. Till exempel, b1=4, q=-2. Dessa två villkor ger en geometrisk progression på 4, -8, 16, -32, … .
Om q>0 (q är inte lika med 1), så är progressionen en monoton sekvens. Till exempel är sekvensen 2, 4,8,16,32, ... en monotont ökande sekvens (b1=2, q=2).
Om nämnaren q=1 i det geometriska felet kommer alla medlemmar av den geometriska progressionen att vara lika med varandra. I sådana fall sägs progressionen vara en konstant sekvens.
För att den numeriska sekvensen (bn) ska vara en geometrisk progression, är det nödvändigt att var och en av dess medlemmar, med början från den andra, är det geometriska medelvärdet av de angränsande delarna. Det vill säga, det är nödvändigt att uppfylla följande ekvation
(b(n+1))^2 = bn * b(n+2), för valfri n>0, där n tillhör mängden naturliga tal N.
Låt oss nu sätta (Xn) - en geometrisk progression. Nämnaren för den geometriska progressionen q, med |q|∞).
Om vi nu betecknar summan av en oändlig geometrisk progression med S, så kommer följande formel att gälla:
S=xl/(1-q).
Tänk på ett enkelt exempel:
Hitta summan av en oändlig geometrisk progression 2, -2/3, 2/9, - 2/27, ... .
För att hitta S använder vi formeln för summan av en oändligt aritmetisk progression. |-1/3|< 1. x1 = 2. S=2/(1-(-1/3)) = 3/2.


