Abstrakt na téma inverzní funkce. Vzájemně inverzní funkce. Vysvětlení nového materiálu

Poznámky k lekci na téma „Inverzní funkce“

Lekce 1. Přednáška na dané téma "Inverzní funkce"

Cílová: Vytvořte si teoretický aparát na dané téma. Vstupte

Pojem reverzibilní funkce;

Pojem inverzní funkce;

Formulujte a dokažte dostatečnou podmínku pro reverzibilitu

funkce;

Základní vlastnosti vzájemně inverzních funkcí.

Plán lekce přednášek

Organizace času.

Aktualizace znalostí studentů nezbytných pro vnímání nového tématu.

Prezentace nového materiálu.

Shrnutí lekce.

Průběh lekce-přednášky

1. Organizace času.

2. Aktualizace znalostí. ( Frontální průzkum na téma předchozí lekce.)

Pro studenty na interaktivní tabule je znázorněn graf funkce (obr. 1). Učitel zformuluje úkol – zvažte graf funkce a vypište prostudované vlastnosti funkce. Studenti vyjmenují vlastnosti funkce v souladu s výzkumným designem. Učitel vpravo od grafu funkce zapíše fixou na interaktivní tabuli jmenované vlastnosti.

Rýže. 1

Vlastnosti funkce:

3. Stanovení cílů pro studenty.

Na konci studia vyučující hlásí, že se dnes v hodině seznámí s další vlastností funkce - reverzibilitou. Pro smysluplné prostudování nové látky vyzve učitel děti, aby se seznámily s hlavními otázkami, na které musí studenti na konci hodiny odpovědět. Otázky ve formuláři letáky Každý žák má jeden (rozdělený před vyučováním).

otázky:

1. Která funkce se nazývá invertibilní?

2. Která funkce se nazývá inverzní?

3. Jak spolu souvisí definiční obory a množiny hodnot přímých a inverzních funkcí?

4. Formulujte postačující podmínku pro invertibilitu funkce.

5. Je inverzní funkce rostoucí funkce klesající nebo rostoucí?

6. Je inverzní funkce k liché funkci sudá nebo lichá?

7. Jak jsou uspořádány grafy vzájemně inverzních funkcí?

4. Prezentace nového materiálu.

1) Pojem invertibilní funkce. Dostatečný stav pro reverzibilitu.

Na interaktivní tabuli učitel porovná grafy dvou funkcí, jejichž definiční obory a množiny hodnot jsou stejné, ale jedna z funkcí je monotónní a druhá ne (obr. 2). Funkce má tedy vlastnost, která není pro funkci charakteristická: jakékoli číslo z množiny funkčních hodnotF ( X ) bez ohledu na to je to hodnota funkce pouze v jednom bodě, čímž učitel vede studenty k pojmu invertibilní funkce.

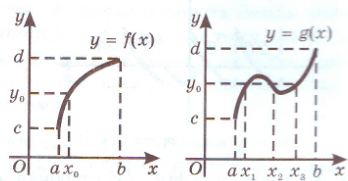
Rýže. 2

Učitel poté zformuluje definici invertibilní funkce a provede důkaz věty o invertibilní funkci pomocí grafu monotónní funkce na interaktivní tabuli.

Definice 1. Funkce je volánareverzibilní , pokud nabývá některou ze svých hodnot pouze v jednom bodě množinyX .

Teorém. Pokud je funkce na sadě monotónníX , pak je reverzibilní.

Důkaz:

Nechte funkci y=f(x) se na setu zvyšujeX nech to být X 1 ≠х 2 – dva body sadyX .

Abychom byli konkrétní, nechX 1 < X 2 . Pak z toho, žeX 1 < X 2 z důvodu zvýšení funkce z toho vyplývá, žef(x 1 ) < f(x 2 ) .

Odpovídají tedy různé hodnoty argumentu různé významy funkce, tzn. funkce je invertibilní.

Obdobně se věta dokazuje v případě klesající funkce.

(Jak postupuje dokazování věty, učitel použije fix, aby na výkrese udělal všechna potřebná vysvětlení)

Před formulováním definice inverzní funkce učitel požádá studenty, aby určili, která z navržených funkcí je invertibilní? Interaktivní tabule zobrazuje grafy funkcí (obr. 3, 4) a zapisuje několik analyticky definovaných funkcí:

A ) b )

Rýže. 3 Obr. 4

PROTI ) y = 2x + 5; G ) y = - + 7.

Komentář. Monotónnost funkce jedostatečný podmínkou pro existenci inverzní funkce. Ale tonení nutná podmínka.

Učitel uvádí příklady různých situací, kdy funkce není monotónní, ale vratná, kdy funkce není monotónní a nevratná, kdy je monotónní a vratná.

2) Pojem inverzní funkce. Algoritmus pro skládání inverzní funkce.

Definice 2. Nechť funguje invertibilníy=f(x) definované na saděX a jeho rozsah hodnotE(f)=Y . Srovnejme každý z nichy z Y to je jediný významX, při kterém f(x)=y. Pak dostaneme funkci, která je definována naY, A X – rozsah funkčních hodnot. Tato funkce je určenax=f -1 (y), a zavolejte zvrátit ve vztahu k funkciy=f(x), .

Poté učitel seznámí studenty s metodou hledání inverzní funkce dané analyticky.

Algoritmus pro skládání inverzní funkce pro funkci y = F ( X ), .

Ujistěte se, že funkcey=f(x) vratné na intervaluX .

Expresní proměnnáX přes na z rov. y=f(x), s přihlédnutím k tomu.

Ve výsledné rovnosti si místa vyměňteX A na. Namísto x=f -1 (y) napsat y=f -1 (X).

Na konkrétních příkladech učitel ukazuje, jak tento algoritmus používat.

Příklad 1 Ukažte to pro funkciy=2x-5

Řešení . Lineární funkce y=2x-5 určeno na R, zvyšuje o R a jeho rozsah hodnot jeR. To znamená, že inverzní funkce existujeR . Abychom našli její analytické vyjádření, řešíme rovniciy=2x-5 poměrně X ; dostaneme to. Přejmenujme proměnné a získáme požadovanou inverzní funkci. Je definován a narůstá na R.

Příklad 2 Ukažte to pro funkciy=x 2 , x ≤ 0 existuje inverzní funkce a najděte její analytické vyjádření.

Řešení . Funkce je spojitá, monotónní ve své oblasti definice, proto je invertibilní. Po analýze domén definice a sad hodnot funkce je učiněn odpovídající závěr o analytickém výrazu pro inverzní funkci, která má tvar.

3) Vlastnosti vzájemně inverzních funkcí.

Nemovitost 1. Li G – funkce inverzní k F , pak F – funkce inverzní k G (funkce jsou vzájemně inverzní), zatímcoD ( G )= E ( F ), E ( G )= D ( F ) .

Nemovitost 2. Pokud funkce roste (klesá) na množině X a Y je rozsah hodnot funkce, pak se inverzní funkce zvyšuje (snižuje) na Y.

Nemovitost 3. Chcete-li získat graf funkce, která je inverzní k funkci, musíte graf funkce transformovat symetricky vzhledem k přímcey=x .

Nemovitost 4. Pokud je lichá funkce invertibilní, pak je její inverzní také lichá.

Nemovitost 5. Pokud funkce F ( X ) A vzájemně inverzní, pak to platí pro kohokoli a platí to pro všechny.

Příklad 3 Pokud je to možné, nakreslete graf inverzní funkce.

Řešení. V celé své definiční oblasti tuto funkci nemá inverzní, protože není monotónní. Uvažujme tedy interval, ve kterém je funkce monotónní: to znamená, že existuje inverzní. najdemejejí . K tomu vyjadřujemeX přesy : . Přejmenujme ji na inverzní funkci. Nakreslete funkce (obr. 5) a ujistěte se, že jsou symetrické vzhledem k přímcey = X .

Rýže. 5

Příklad 4. Najděte sadu hodnot každé z recipročních funkcí, pokud je to známo.

Řešení. Podle vlastnosti 1 vzájemně inverzních funkcí máme.

5 . Shrnutí

Provádění diagnostické práce. Účelem této práce je zjistit úroveň asimilace vzdělávací materiál diskutováno na přednášce. Studenti jsou požádáni, aby odpověděli na otázky formulované na začátku přednášky.

6 . Inscenace domácí práce.

1. Porozumět probrané látce, naučit se základní definice a tvrzení vět.

2. Dokažte vlastnosti vzájemně inverzních funkcí.

Lekce 2. Workshop na téma „Definice inverzní funkce. Dostatečná podmínka pro invertibilitu funkce"

Cílová: rozvíjet schopnost aplikovat teoretické znalosti na dané téma při řešení úloh, uvažovat o hlavních typech úloh pro studium funkce pro reverzibilitu, pro konstrukci inverzní funkce.

Plán lekce workshopu:

1. Organizační moment.

2. Aktualizace znalostí (přední práce studentů).

3. Upevňování probrané látky (řešení úloh).

4. Shrnutí lekce.

5. Zadání domácího úkolu.

Během vyučování.

1. Organizace času.

Pozdrav učitele, kontrola připravenosti žáků na hodinu.

2. Aktualizace znalostí. ( frontální práce studentů).

Studenti jsou požádáni, aby ústně dokončili následující úkoly:

1. Formulujte postačující podmínku pro invertibilitu funkce.

2. Mezi funkcemi, jejichž grafy jsou znázorněny na obrázku, označte ty, které jsou reverzibilní.

3. Formulujte algoritmus pro sestavení funkce inverzní k dané funkci.

4. Existují datové inverzní funkce? Pokud je odpověď ano, najděte je:

A) ; b ) ; C ) .

5. Jsou funkce, jejichž grafy jsou znázorněny na obrázku, vzájemně inverzní (obr. 6)? Zdůvodněte svou odpověď.

Rýže. 6

3. Upevňování probrané látky (řešení problémů).

Konsolidace studovaného materiálu se skládá ze dvou fází:

Individuální samostatná práce studenti;

Shrnutí výsledků samostatné práce.

V první fázi jsou studentům nabídnuty karty s úkoly, které plní samostatně.

Cvičení 1.

Jsou funkce invertovatelné v celé jejich doméně? Pokud ano, najděte k němu opak.

A) ; b) ; c).

Úkol 2.

Jsou funkce vzájemně inverzní?

A);

b ) .

Úkol 3.

Uvažujme funkci na každém z uvedených intervalů; pokud je na tomto intervalu funkce invertibilní, definujte její inverzní analyticky, uveďte definiční obor a rozsah hodnot:

A ) R ; b ) ; d ) [-2;0].

Úkol 4.

Dokažte, že funkce je nevratná. Najděte inverzní funkci na intervalu a vykreslete její graf.

Úkol 5.

Nakreslete graf funkce a určete, zda pro ni existuje inverzní funkce. Pokud ano, vykreslete inverzní funkci do stejného výkresu a definujte ji analyticky:

A ) ; b ) .

Ve fázi sčítání výsledků samostatné práce studentů jsou úkoly kontrolovány pouze se záznamem průběžných výsledků. Problémy, které způsobily největší potíže, jsou zvažovány na tabuli, buď odhalují hledání řešení, nebo zaznamenávají celé řešení.

4. Shrnutí lekce (reflexe).

Studentům je k dispozici minidotazník:

Co se mi na lekci líbilo?_______________________________

Co se mi na lekci nelíbilo?_______________________________

_________________________________________________________________

Uveďte prosím jedno tvrzení, které vám nejlépe vyhovuje:

1) Dokážu nezávisle zkoumat reverzibilitu funkce, sestrojit její inverzní hodnotu a jsem si jistý správností výsledku.

2) Umím zkoumat funkci na invertibilitu, zkonstruovat její inverzi, ale nejsem si vždy jist správností výsledku, potřebuji pomoc svých přátel.

3) Funkci pro reverzibilitu prakticky nemohu nastudovat, sestrojit inverzní, potřebuji další radu od učitele.

Kde mohu uplatnit získané znalosti?_____________________ ____________________________________________________________________

5. Nastavení domácího úkolu.

№ 10,3, 10,6 (c, d), 10,7 (c, d), 10,9 (c, d), 10,13 (c, d), 10,18.(Mordkovich, A.G. Algebra a počátky matematické analýzy 10. ročník. Ve 14 hodin 2. část. Problémová kniha pro studenty vzdělávací instituce (úroveň profilu) / A.G. Mordkovich, P.V. Semenov. - M.: Mnemosyne, 2014. - 384 s.)

I. Komunikace tématu a účelu lekce

II. Opakování a upevňování probrané látky

1. Odpovědi na otázky k domácím úkolům (rozbor nevyřešených problémů).

2. Sledování asimilace materiálu (samostatná práce).

Možnost 1

Možnost 2

Prozkoumejte funkci a zakreslete ji do grafu:

III. Učení nového materiálu

Pomocí analytického tvaru funkce lze pro libovolnou hodnotu argumentu snadno najít odpovídající hodnotu funkce y. Často nastává inverzní problém: hodnota y je známá a je nutné najít hodnotu argumentu X , při kterém je dosaženo.

Příklad 1

Najdeme hodnotu argumentu x, pokud je hodnota funkcerovná se: a) 2; b) 7/6; v 1.

Z analytické formy funkcevyjádřete proměnnou x a získejte: 4 xy - 2y = 3 x + 1 nebo x(4y - 3) = 2y + 1, odkud. Nyní je snadné problém vyřešit:

Funkce nazýváme inverzní funkci. Protože je obvyklé označovat argument funkce písmenem x a hodnotu funkce písmenem y, zapisuje se inverzní funkce ve tvaru

Dáme pojmy potřebné ke studiu tématu.

Definice 1. Funkce y = f(x), x ∈ X se nazývá invertibilní, pokud nabývá některou ze svých hodnot pouze v jednom bodě x množiny X (jinými slovy, pokud různé hodnoty argumentu odpovídají různým hodnotám funkce). V opačném případě se funkce nazývá nevratná.

Příklad 2

Funkce Každá z jeho hodnot nabývá pouze jednoho bodu x a je vratná (graf a). Funkcemá hodnoty y (například y = 2), kterých je dosaženo ve dvou různých bodech X a je nevratná (graf b).

Následující věta je užitečná při zvažování tématu.

Věta 1. Jestliže funkce y = f (x), x ∈ X je monotónní na množině X, pak je invertibilní.

Příklad 3

Vraťme se k předchozímu příkladu. Funkceklesá (monotónní) a je invertibilní v celé oblasti definice. Funkcenemonotónní a nevratné. Tato funkce však narůstá na intervalech (-∞; -1] a . Proto je na takových intervalech funkce invertibilní. Například funkce je invertibilní na intervalu x ∈ [-1; 1].

Definice 2. Nechť y = f (x), x ∈ X je invertibilní funkce a E(f) = Y . Srovnejme každý z nich Y je jedinou hodnotou x, pro kterou f(x ) = y (tj. jediný kořen rovnice f(x ) = y vzhledem k proměnné x). Pak dostaneme funkci, která je definována na množině Y (množina X je její rozsah hodnot). Tato funkce je označena x – f-1 (y), y ∈ Y a nazývá se inverzí funkce y = f (x), x ∈ X. Obrázek ukazuje funkci y = F (x) a inverzní funkce x = f-1 (y).

Dopředná a inverzní funkce mají stejnou monotónnost.

Věta 2. Jestliže funkce y = F (x) roste (klesá) na množině X a Y je její rozsah hodnot, pak inverzní funkce x = f-1 (y ) zvyšuje (snižuje) na televizoru Y.

Příklad 4

Funkce na setu klesáa má mnoho významůInverzní funkcena sadě také klesáa má mnoho významůPochopitelně grafy funkcí A se shodují, protože tyto funkce vedou ke stejnému vztahu mezi proměnnými x a y: 4xy - 3x - 2y - 1 = 0.

U nás je zvykem, že argument funkce se značí písmenem x a hodnota funkce písmenem y. Proto budeme inverzní funkci psát ve tvaru y = f -1 (x) (viz příklad 1).

Věta 3. Grafy funkce y = F (x) a inverzní funkce y = f-1 symetrická k relativní přímce y = x.

Příklad 5

Pro funkci y = 2x - 4 najdeme inverzní funkci: y + 4 = 2x, odkud x = 1/2y + 2. Zaveďme redesignace x↔ y a zapište inverzní funkci ve tvaru y = 1/2x + 2. Tedy pro funkci F (x) = 2x – 4 inverzní funkce f-1(x ) = 1/2х + 2. Sestavme grafy těchto funkcí. Je vidět, že grafy jsou symetrické k relativní přímce y = x.

Funkce f -1 (x ) = 1/2x + 2 inverze funkce F (x) = 2x - 4. Ale také funkce F (x) = 2x - 4 je inverzní funkce f-1(x ) = 1/2x + 2. Proto funkce f(x) a f-1 (x) se správněji nazývá reciproční. V tomto případě jsou splněny následující rovnosti: f-1 (f (x)) = x af (f-1 (x) = x.

IV. Kontrolní otázky

1. Reverzibilní a nevratné funkce.

2. Invertibilita monotónní funkce.

3. Definice inverzní funkce.

4. Monotonie přímých a inverzních funkcí.

5. Grafy přímých a inverzních funkcí.

V. Zadání lekce

§ 3, č. 1 (a, b); 2 (c, d); 3 (a, d); 4 (c, d); 5 (a, c).

VI. Zadání domácího úkolu

§ 3, č. 1 (c, d); 2 (a, b); 3 (b, c); 4 (a, b); 5 (b, d).

VII. Shrnutí lekce

Cíle lekce:

Vzdělávací:

• stavět na znalostech nové téma v souladu s programovým materiálem;
• studovat vlastnost reverzibility funkce a učit, jak najít inverzní funkci dané funkce;

Vývojový:

• rozvíjet schopnosti sebeovládání, věcnou řeč;
• osvojit si pojem inverzní funkce a naučit se metody hledání inverzní funkce;

Vzdělávací: rozvíjet komunikativní kompetence.

Zařízení: počítač, projektor, plátno, interaktivní tabule SMART Board, písemky (samostatná práce) pro skupinovou práci.

Během vyučování.

1. Organizační moment.

cílová – příprava studentů na práci ve třídě:

Definice nepřítomných,

Naladit studenty na práci, organizovat pozornost;

Uveďte téma a účel lekce.

2. Aktualizace základních znalostí studentů. Frontální průzkum.

Cílová - zjistit správnost a informovanost probrané teoretické látky, opakování probrané látky.<Приложение 1 >

Na interaktivní tabuli pro studenty je zobrazen graf funkce. Učitel zformuluje úkol – zvažte graf funkce a vypište prostudované vlastnosti funkce. Studenti vyjmenují vlastnosti funkce v souladu s výzkumným designem. Učitel vpravo od grafu funkce zapíše fixou na interaktivní tabuli jmenované vlastnosti.

Vlastnosti funkce:

Na konci studia vyučující hlásí, že se dnes v hodině seznámí s další vlastností funkce - reverzibilitou. Pro smysluplné prostudování nové látky vyzve učitel děti, aby se seznámily s hlavními otázkami, na které musí studenti na konci hodiny odpovědět. Otázky jsou napsány na běžné tabuli a každý student je má jako podklady (rozdané před lekcí)

1. Která funkce se nazývá invertibilní?
2. Je nějaká funkce invertovatelná?
3. Která funkce se nazývá inverzní k nulovému bodu?
4. Jak spolu souvisí definiční obor a množina hodnot funkce a její inverzní vztah?
5. Pokud je funkce dána analyticky, jak lze definovat inverzní funkci vzorcem?
6. Pokud je funkce zadána graficky, jak znázornit její inverzní funkci?

3. Vysvětlení nového materiálu.

cílová - vytvářet znalosti na nové téma v souladu s programovým materiálem; studovat vlastnost reverzibility funkce a učit, jak najít inverzní funkci dané funkce; rozvíjet věcnou řeč.

Učitel prezentuje látku v souladu s látkou v odstavci. Učitel na interaktivní tabuli porovná grafy dvou funkcí, jejichž definiční obory a množiny hodnot jsou stejné, ale jedna z funkcí je monotónní a druhá ne, čímž seznámí studenty s konceptem invertibilní funkce. .

Učitel poté zformuluje definici invertibilní funkce a provede důkaz věty o invertibilní funkci pomocí grafu monotónní funkce na interaktivní tabuli.

Definice 1: Je volána funkce y=f(x), x X reverzibilní, pokud nabývá některou ze svých hodnot pouze v jednom bodě množiny X.

Věta: Je-li funkce y=f(x) monotónní na množině X, pak je invertibilní.

Důkaz:

1. Nechte funkci y=f(x) zvyšuje o X nech to být x 1 ≠ x 2- dva body setu X.
2. Abychom byli konkrétní, nech x 1< x 2.
   Pak z toho, že x 1< x 2 to následuje f(x 1) < f(x 2).
3. Různé hodnoty argumentu tedy odpovídají různým hodnotám funkce, tj. funkce je invertibilní.

(Jak postupuje dokazování věty, učitel použije fix, aby na výkrese udělal všechna potřebná vysvětlení)

Před formulováním definice inverzní funkce učitel požádá studenty, aby určili, která z navržených funkcí je invertibilní? Interaktivní tabule zobrazuje grafy funkcí a zapisuje několik analyticky definovaných funkcí:

b)

G) y = 2x + 5

D) y = -x2 + 7

Učitel představí definici inverzní funkce.

Definice 2: Nechť funguje invertibilní funkce y=f(x) definované na sadě X A E(f)=Y. Srovnejme každý z nich y z Y to je jediný význam X, při kterém f(x)=y. Pak dostaneme funkci, která je definována na Y, A X– funkční rozsah

Tato funkce je určena x=f -1 (y) a nazývá se inverzní funkce y=f(x).

Studenti jsou požádáni, aby vyvodili závěr o spojení mezi definičním oborem a množinou hodnot inverzních funkcí.

K zamyšlení nad otázkou, jak najít inverzní hodnotu dané funkce, učitel přilákal dva studenty. Den předem dostaly děti od učitele úkol samostatně analyzovat analytické a grafické metody hledání inverzní funkce dané funkce. Učitel působil jako konzultant při přípravě studentů na hodinu.

Zpráva od prvního studenta.

Poznámka: monotónnost funkce je dostatečný podmínkou pro existenci inverzní funkce. Ale to není nutná podmínka.

Žák uvedl příklady různých situací, kdy funkce není monotónní, ale invertibilní, kdy funkce není monotónní a není invertibilní, kdy je monotónní a invertibilní.

Student poté seznámí studenty s metodou hledání inverzní funkce dané analyticky.

Algoritmus hledání

1. Ujistěte se, že funkce je monotónní.
2. Vyjádřete proměnnou x pomocí y.
3. Přejmenovat proměnné. Místo x=f -1 (y) napište y=f -1 (x)

Poté vyřeší dva příklady, aby našel inverzní funkci daného.

Příklad 1: Ukažte, že pro funkci y=5x-3 existuje inverzní funkce a najděte její analytické vyjádření.

Řešení. Lineární funkce y=5x-3 je definována na R, roste na R a její rozsah hodnot je R. To znamená, že na R existuje inverzní funkce. Chcete-li najít její analytické vyjádření, vyřešte rovnici y=5x- 3 pro x; dostaneme Toto je požadovaná inverzní funkce. Je definován a narůstá na R.

Příklad 2: Ukažte, že pro funkci y=x 2, x≤0 existuje inverzní funkce, a najděte její analytické vyjádření.

Funkce je spojitá, monotónní ve své oblasti definice, proto je invertibilní. Po analýze domén definice a sad hodnot funkce je učiněn odpovídající závěr o analytickém výrazu pro inverzní funkci.

Druhý student udělá prezentaci o grafický metoda hledání inverzní funkce. Při svém výkladu žák využívá možností interaktivní tabule.

Pro získání grafu funkce y=f -1 (x), inverzní k funkci y=f(x), je nutné transformovat graf funkce y=f(x) symetricky vzhledem k přímce. y=x.

Během výkladu na interaktivní tabuli se plní následující úkol:

Sestrojte graf funkce a graf její inverzní funkce ve stejném souřadnicovém systému. Zapište si analytický výraz pro inverzní funkci.

4. Primární konsolidace nového materiálu.

Cílová - zjistit správnost a povědomí o porozumění studovanému materiálu, identifikovat mezery v primárním porozumění materiálu a opravit je.

Studenti jsou rozděleni do dvojic. Dostanou listy úkolů, ve kterých dělají práci ve dvojicích. Čas na dokončení práce je omezený (5-7 minut). Jedna dvojice studentů pracuje na počítači, projektor se během této doby vypne a ostatní děti nevidí, jak studenti na počítači pracují.

Po uplynutí času (předpokládá se, že většina studentů práci dokončila) se práce studentů zobrazí na interaktivní tabuli (zapne se opět projektor), kde se při kontrole zjistí, zda úkol byla dokončena správně ve dvojicích. V případě potřeby učitel provádí korekční a výkladové práce.

Samostatná práce ve dvojicích<Dodatek 2 >

5. Shrnutí lekce. K otázkám, které byly položeny před přednáškou. Vyhlášení známek na lekci.

Domácí úkol §10. Č. 10,6(a,c) 10,8-10,9(b) 10,12 (b)

Algebra a počátky analýzy. Stupeň 10 Ve 2 částech pro instituce všeobecného vzdělávání (úroveň profilu) / A.G. Mordkovich, L.O. Denishcheva, T.A. Koreshkova atd.; upravil A.G. Mordkovich, M: Mnemosyne, 2007

Inverzní funkce

Text lekce

• Poznámky lekce 1-3 (Morozova I. A.)

  Název předmětu Algebra a počátky matematické analýzy Třída 10 UMK Algebra a počátky matematické analýzy. 10-11 tříd. Ve 2 hodiny Část 1. Učebnice pro studenty všeobecně vzdělávacích institucí ( základní úroveň)/ A.G. Mordkovič. – 10. vyd., vymazáno. – M.: Mnemosyne, 2012. Část 2. Problémová kniha pro studenty všeobecně vzdělávacích institucí (základní úroveň) / [A.G. Mordkovich et al]; upravil A.G. Mordkovič. – 10. vyd., vymazáno. – M.: Mnemosyne, 2012. Základní úroveň učení Téma lekce: Inverzní funkce. (3 hodiny) Lekce 1. Cíl lekce: představit pojmy reverzibilní a inverzní funkce; provést důkaz věty o monotónnosti přímých a inverzních funkcí; identifikovat a zdůvodnit geometrický význam reverzibilita funkce Cíle lekce: - rozvinout schopnost najít inverzní funkci pro danou funkci; - rozvíjet schopnost sestavit graf inverzní funkce. Plánované výsledky: Znát: definici vratné funkce, inverzní funkce, znaménko vratnosti funkce. Umět: najít vzorec pro funkci inverzní k dané funkci; sestavte graf inverzní funkce pomocí grafu dané funkce. Technická podpora lekce: počítač, plátno, projektor, učebnice. Průběh lekce I. Organizační moment. II. Kontrola domácích úkolů (rozbor úkolů, které žákům působily potíže) III. Ověřovací práce. Možnost 1 1. Je dána funkce a) Zjistěte monotónnost funkce, pokud x > 2. b) Najděte největší a nejmenší hodnotu funkce na intervalu [–1,5; 1,5]. 2. Prozkoumejte funkci kde x > 0 pro omezenost. 3. Zkontrolujte paritu funkce. Možnost 2 1. Je dána funkce a) Zjistěte monotónnost funkce, jestliže x< 2. б) Найдите наибольшее и наименьшее значения функции на отрезке [–4,5; –3,1]. 2. Исследуйте функцию где х < 0, на ограниченность. 3. Исследуйте функцию на четность. Вариант 3 1. Дана функция а) Исследуйте функцию на монотонность, если х < –1. б) Найдите наибольшее и наименьшее значения функции на отрезке [–2; 0,4]. 2. Исследуйте функцию где х < –1, на ограниченность. 3. Исследуйте функцию на четность. Вариант 4 1. Дана функция а) Исследуйте функцию на монотонность, если х  1. б) Найдите наибольшее и наименьшее значения функции на отрезке . 2. Исследуйте функцию где х >2, pro omezení. 3. Zkontrolujte paritu funkce. Řešení možností 1 a 3 zkušební práce. Možnosti 1 a 2 jsou o něco snazší než možnosti 3 a 4. Možnost 1 1. Označme a) Nechme funkci zmenšit o (–; 2]. b) Protože funkce klesá o (–∞; 2], pak Odpověď: a) klesá ; b) unaib. = 12,25; zamířit. = 0,25. 2. kde x > 0. Funkce je shora omezena přímkou ​​y = 0, což znamená, že funkce je shora omezena přímkou ​​y = 1. Odpověď: ohraničená výše. 3. – symetrické podle původu. To znamená, že funkce je lichá. Odpověď: liché. Možnost 3 1. a) Označme Graf jako parabolu s vrcholem v bodě (–1; –1) a protínající osu 0x v bodech x = 0 a x = –2. Pokud x > –1, pak se funkce zvýší. b) Na segmentu [–2; 0,4] a odpověď: a) zvyšuje; b) unaib. = 0,96; zamířit. = 0. 2. kde x< –1. Функция ограничена снизу прямой у = 0, значит, функция ограничена снизу прямой у = 2. Ответ: ограничена снизу. 3. – симметрична относительно начала координат. Если х = 0, то Имеем: значит, функция ни четная, ни нечетная. Ответ: ни четная, ни нечетная. IV. Объяснение нового материала. 1. Для введения понятия обратимой функции можно использовать либо подвижные модели, либо изображение обратимых и необратимых функций на прозрачной пленке, перевернув которую можно показать, как область определения и область значения функции «меняются местами» и в каком случае обеспечивается однозначность обратной функции. 2. Для первичного закрепления материала учащиеся выполняют следующее задание. Среди функций, графики которых изображены на рисунке, укажите обратимые. 3. Теорема 1. Подчеркиваем учащимся, что в теореме сформулирован признак обратимости функции (достаточное условие). В то же время монотонность не является необходимым условием обратимости. Динамическая пауза. V. Формирование умений и навыков. Упражнения, решаемые на этом уроке, направлены на аналитическое задание функции, обратной данной. № 3.1 (а; б), № 3. 2 (а; б). При выполнении этих упражнений следует предупредить формализм в аналитическом задании функции путем простого преобразования уравнения. Учащиеся должны обосновать существование обратной функции. Решение: № 3.1 (б). Линейная функция у = 2 + 4х определена на R, возрастает на R(k  0), E(f) = R. Значит, на R существует обратная функция. – искомая обратная функция, возрастающая на R. Ответ: № 3.2 (б). Функция убывает на всей области определения, значит, существует обратная функция, определенная и убывающая на Ответ: V. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. Домашнее задание: № 3.1 (в; г) – № 3.2 (в; г). Урок 2. Цель урока: выявить и обосновать геометрический смысл обратимости функции Задачи урока: - развивать умение находить обратную функцию для заданной; - формировать умение строить график обратной функции. Планируемые результаты: Знать: определение обратимой функция, обратной функции, признак обратимости функции. Уметь: находить формулу функции, обратной данной; строить график обратной функции, используя график данной функции. Техническое обеспечение урока компьютер, экран, проектор, учебник. Ход урока I. Организационный момент. II. Проверка домашнего задания (разбор заданий, вызвавших затруднения учащихся) III. Работа в группах. Карточка 1. Карточка 2. IV. Объяснение нового материала. Устанавливая геометрический смысл обратимости функции, учащиеся формулируют способ построения графика обратной функции с помощью преобразования осевой симметрии. Графики функции у = f(х) и обратной функции у = f-1 симметричны относительной прямой у = х. Для функции у = 2х - 4 найдем обратную функцию: у + 4 = 2х, откуда х = 1/2у + 2. Введем переобозначения х ↔ у и запишем обратную функцию в виде у = 1/2х + 2. Таким образом, для функции f(х) = 2х – 4 обратная функция f-1(x) = 1/2х + 2. Построим графики этих функций. Видно, что графики симметричны относительной прямой у = х. Функция f-1(x) = 1/2х + 2 обратная по отношению к функции f(х) = 2х - 4. Но и функция f(х) = 2х - 4 является обратной по отношению к функции f-1(x) = 1/2х + 2. Поэтому функции f(х) и f-1(х) корректнее называть взаимообратными. При этом выполнены равенства: f-1(f(х)) = х и f(f-1(x) = x. Динамическая пауза. V. Формирование умений и навыков. Упражнения, решаемые на этом уроке, направлены на построение графика обратной функции с помощью осевой симметрии. № 3.3 (а; б), № 3. 4 (а; б), № 3.5* (а; б). Решение: № 3. 4 (б). Графиком является кубическая парабола, полученная из графика у = х3 сдвигом вправо по оси 0х на 2 единицы. Функция возрастает на R, значит, существует обратная функция, заданная и возрастающая на R. Ответ: V. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. – Каков характер монотонности прямой и обратной функций? – Как построить график обратной функции, используя график данной функции? Домашнее задание: № 3.3 (в; г) – № 3.4 (в; г) № 3.5 * (в; г) – по желанию. Урок 3. Цель урока: проверить степень усвоения теоретического материала и умения применять его при выполнении письменной работы Задачи урока: - развивать умение находить обратную функцию для заданной; - развивать умение строить график обратной функции. Планируемые результаты: Знать: определение обратимой функция, обратной функции, признак обратимости функции. Уметь: находить формулу функции, обратной данной; строить график обратной функции, используя график данной функции. Техническое обеспечение урока компьютер, экран, проектор, учебник. Ход урока I. Организационный момент. II. Проверка домашнего задания (разбор заданий, вызвавших затруднения учащихся) III. Зачетная работа Вариант 1. Вариант 2. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. – Каков характер монотонности прямой и обратной функций? – Как построить график обратной функции, используя график данной функции? Домашнее задание: §3, примеры 1-3.

  Stáhnout: Algebra 10kl - Poznámky lekce 1-3 (Morozova I. A.).docx

• Lekce 1 (Samoilova G. A.)

  Algebra a počátky 10. stupně analýzy UMC: Algebra a počátky 10.–11. stupně analýzy, A.G. Mordkovich, Moskva 2013 Úroveň učení: základní Téma: Inverzní funkce Celkový počet hodin: 3 hodiny K tématu: lekce č. 1 Účel lekce: Vzdělávací: Představit a upevnit definici inverzní funkce; studovat vlastnost reverzibility funkce a učit, jak najít inverzní funkci dané funkce; Vývojové: rozvíjet schopnosti sebeovládání, věcnou řeč; osvojit si pojem inverzní funkce a naučit se metody hledání inverzní funkce; Vzdělávací: rozvíjet komunikativní kompetence. Cíle hodiny: 1. Seznámit studenty s invertibilními funkcemi a jejich grafy. 2. Obohaťte zkušenosti studentů při získávání nových znalostí na základě dosavadních teoretických znalostí a také využitím známých praktických situací Plánované výsledky: Po prostudování tohoto tématu by studenti měli znát: Definici invertibilní funkce; vykreslení reverzibilní funkce; příklady funkcí ze života; techniky srovnávání, zobecňování, schopnost vyvozovat závěry; Po prostudování tohoto tématu by studenti měli být schopni: samostatně si doplňovat a systematizovat znalosti: - sestavovat grafy vratných funkcí: - umět vyvozovat závěry. Technická podpora lekce: tutorial„Algebra a počátky analýzy. 10. třída (základní úroveň)“ A.G. Mordkovič. Tabulky numerické funkce . Počítač, projektor, plátno. Doplňková metodická a didaktická podpora hodiny: Metodická příručka pro učitele „Plány hodin k učebnici Algebra a začátek rozboru ročníky 10-11“, A.G. Mordkovich, Volgograd 2013 Internetové zdroje https:// 1september.ru Obsah lekce: 1. Organizační moment 2. Kontrola zbytkových znalostí 3. Studium nového materiálu 4. Upevňování 5. Shrnutí lekce 6. Stanovení domácích úkolů Průběh lekce: 1. Organizační bod 2 Kontrola zbytkových znalostí 1). Opakování a upevňování probrané látky 1. Odpovědi na otázky k domácím úkolům (rozbor nevyřešených problémů). 2. Sledování asimilace materiálu (samostatná práce). Možnost 1 Proveďte studii funkce a vytvořte její graf: 3. Studium nového materiálu Pomocí analytické formy funkce lze pro jakoukoli hodnotu argumentu snadno najít odpovídající hodnotu funkce y. Často nastává inverzní problém: hodnota y je známá a je nutné najít hodnotu argumentu x, při které je dosaženo. Příklad 1 Najděte hodnotu argumentu x, pokud je hodnota funkce rovna: a) 2; b) 7/6; c) 1. Z analytického tvaru funkce vyjádříme proměnnou x a dostaneme: 4xy - 2y = 3x + 1 nebo x(4y - 3) = 2y + 1, odkud. Nyní je snadné problém vyřešit: Funkce se nazývá inverzní funkce. Protože je zvykem označovat argument funkce písmenem x a hodnotu funkce písmenem y, zapisuje se inverzní funkce ve tvaru Uveďme si pojmy potřebné ke studiu tématu. Definice 1. Funkce y = f(x), x ∈ X se nazývá invertibilní, pokud nabývá některou ze svých hodnot pouze v jednom bodě x množiny X (jinými slovy, pokud odpovídají různé hodnoty argumentu na různé hodnoty funkce). V opačném případě se funkce nazývá nevratná. Příklad 2 Funkce nabývá každou hodnotu pouze v jednom bodě x a je vratná (graf a). Funkce má hodnoty y (například y = 2), kterých je dosaženo ve dvou různých bodech x, a je nevratná (graf b). Následující věta je užitečná při zvažování tématu. Věta 1. Je-li funkce y = f(x), ∈ monotónní na množině X, pak je invertibilní. Příklad 3 Vraťme se k předchozímu příkladu. Funkce je klesající (monotónní) a invertibilní v celém definičním oboru. Funkce je nemonotónní a nevratná. Tato funkce však narůstá na intervalech (-∞; -1] a . Proto je na takových intervalech funkce invertibilní. Například funkce je invertibilní na intervalu x [-1;1 ]. Definice 2. Nechť y = f(x), x ∈ X je invertibilní funkce a E(f) = Y. Přiřaďme každému Y jedinečnou hodnotu x, pro kterou f(x) = y (tj. tj. jediný kořen rovnice f(x) = y vzhledem k proměnné x). Pak dostaneme funkci, která je definována na množině Y (množina X je její rozsah hodnot). Tato funkce se značí x – f-1(y), y ∈ Y a nazývá se inverzní funkce y = f(x), x ∈ X. Na obrázku je funkce y = f(x) a inverzní funkce. x = f-l(y). Dopředná a inverzní funkce mají stejnou monotónnost. Věta 2. Jestliže funkce y = f(x) roste (klesá) na množině X a Y je její obor hodnot, pak inverzní funkce x = f-1(y) roste (klesá) na množině Y. Příklad 4 Funkce klesá na množině a má mnoho hodnot. Inverzní funkce také klesá na množině a má mnoho hodnot. Je zřejmé, že grafy funkcí a funkcí se shodují, protože tyto funkce vedou ke stejnému vztahu mezi proměnnými x a y: 4xy - 3x - 2y - 1 = 0. U nás je zvykem, že argument funkce se značí písmenem x a hodnota funkce písmenem y. Inverzní funkci tedy zapíšeme ve tvaru y = f-1(x) (viz příklad 1). Věta 3. Grafy funkce y = f(x) a inverzní funkce y = f-1 jsou symetrické k relativní přímce y = x. Příklad 5 Pro funkci y = 2x - 4 najdeme inverzní funkci: y + 4 = 2x, z čehož x = 1/2y + 2. Zaveďme reoznačení x ↔ y a zapišme inverzní funkci ve tvaru y = 1/2x + 2. Pro funkci f(x) = 2x – 4 je tedy inverzní funkce f-1(x) = 1/2x + 2. Sestavme grafy těchto funkcí. Je vidět, že grafy jsou symetrické k relativní přímce y = x. Funkce f-1(x) = 1/2x + 2 je inverzí funkce f(x) = 2x - 4. Ale funkce f(x) = 2x - 4 je také inverzí funkce f-1 (x) = 1/2x + 2. Proto je správnější nazývat funkce f(x) a f-1(x) reciproké. V tomto případě jsou splněny rovnosti: f-1(f(x)) = x a f(f-1(x) = x. 4. Zesílení 1) Testové otázky: 1. Invertibilní a nevratné funkce. 2. Invertibilita monotónní funkce. 3. Definice inverzní funkce. 4. Monotonie přímých a inverzních funkcí. 5. Grafy přímých a inverzních funkcí. 2) Zadání lekce § 3, č. 1 (a, b); 2 (c, d); 3 (a, d); 4 (c, d); 5 (a, c). 5. Shrnutí lekce Co nového jste se dnes ve třídě naučili? S jakými obtížemi jste se setkali? Udělejte závěr o vztahu mezi doménou definice a množinou hodnot inverzních funkcí. 4. Zadání domácího úkolu § 3, č. 1 (c, d); 2 (a, b); 3 (b, c); 4 (a, b); 5 (b, d).

  Ke stažení: Algebra 10kl - lekce 1 (Samoilova G. A.).doc

• lekce 2 (Samoilova G. A.)

  Algebra a počátky 10. stupně analýzy UMC: Algebra a počátky 10.–11. stupně analýzy, A.G. Mordkovich, Moskva 2013 Úroveň učení: základní Téma: Inverzní funkce Celkový počet hodin: 3 Téma: lekce č. 2 Účel lekce: Vzdělávací: upevnit definici inverzní funkce; upevnit znalosti o vlastnostech reverzibility funkce a naučit, jak najít inverzní funkci dané funkce; Vývojové: rozvíjet schopnosti sebeovládání, věcnou řeč; vlastní metody hledání inverzní funkce; Vzdělávací: rozvíjet komunikativní kompetence; Zorganizujte žákům práci při hledání problémů Cíle hodiny: 1. Seznámit studenty s invertibilními funkcemi a jejich grafy. 2. Obohaťte zkušenosti studentů při získávání nových znalostí na základě dosavadních teoretických znalostí a také využitím známých praktických situací Plánované výsledky: Po prostudování tohoto tématu by studenti měli znát: Definici invertibilní funkce; vykreslení reverzibilní funkce; příklady funkcí ze života; techniky srovnávání, zobecňování. Po prostudování tohoto tématu by studenti měli být schopni: - samostatně si doplňovat a systematizovat znalosti: - sestavovat grafy vratných funkcí: - umět vyvozovat závěry. Technická podpora lekce: učebnice „Algebra a počátky analýzy. 10. třída (základní úroveň)“ A.G. Mordkovič. Tabulky číselných funkcí. Počítač, projektor, plátno. Doplňková metodická a didaktická podpora hodiny: Metodická příručka pro učitele „Plány hodin k učebnici Algebra a začátek rozboru ročníky 10-11“, A.G. Mordkovich, Volgograd 2013 Internetové zdroje https:// 1september.ru Obsah lekce: 1. Organizační moment 2. Kontrola domácích úkolů 3. Upevňování probrané látky 4. Testová práce 5. Shrnutí lekce 6. Zadání domácího úkolu 1. Organizační moment. Učitel sdělí žákům téma, účel hodiny a prostředky, jak toho dosáhnout. 2. Kontrola domácího úkolu 1) Problémy, které způsobují potíže, se řeší u tabule 2) Frontální přehled teoretické části tématu Otázky: 1. Která funkce se nazývá reverzibilní? 2. Je nějaká funkce invertibilní? 3. Která funkce se nazývá inverzní k dané funkci? 4. Jak souvisí definiční obor a množina hodnot funkce a její inverzní funkce? 5. Pokud je funkce dána analyticky, jak lze definovat inverzní funkci vzorcem? 6. Je-li funkce zadána graficky, jak znázornit její inverzní funkci? 3. Konsolidace probraného materiálu 1) Práce na hotovém výkresu (opakování vlastností číselné funkce). Na interaktivní tabuli pro studenty je zobrazen graf funkce. Učitel zformuluje úkol – zvažte graf funkce a vypište prostudované vlastnosti funkce. Studenti vyjmenují vlastnosti funkce v souladu s výzkumným designem. Žák vpravo od grafu funkce zapíše fixou na interaktivní tabuli vyjmenované vlastnosti. Vlastnosti funkce: 1. D(f) = [-4;], E(y) = jak na, tak na [-1;0] 6. ynaib- neexistuje ynaim=0 při x=0 7. xmax = -1 ,ymax = 2 xmin = -2, ymin = 1 xmin = 0, ymin = 0 8. Konvexní dolů na , konvexní nahoru na . 2) Zvažte funkci a najděte její inverzní hodnotu. (Práce u tabule, návrh v sešitu). Daná funkce y=x2,x∈)