Sammanfattning om ämnet omvänd funktion. Ömsesidigt omvända funktioner. Förklaring av nytt material

Lektionsanteckningar om ämnet "Invers av en funktion"

Lektion 1. Föreläsning om ämnet "Omvänd funktion"

Mål: Skapa en teoretisk apparat om ämnet. Stiga på

Konceptet med en reversibel funktion;

Begreppet en invers funktion;

Formulera och bevisa ett tillräckligt villkor för reversibilitet

funktioner;

Grundläggande egenskaper hos ömsesidigt omvända funktioner.

Föreläsning lektionsplan

Att organisera tid.

Uppdatering av elevernas kunskaper som är nödvändiga för att uppfatta ett nytt ämne.

Presentation av nytt material.

Sammanfattning av lektionen.

Lektionens framsteg

1. Att organisera tid.

2. Uppdaterar kunskap. ( Frontal undersökning om ämnet för föregående lektion.)

För studenter på interaktiv whiteboard funktionsdiagrammet visas (fig. 1). Läraren formulerar en uppgift - överväg grafen för en funktion och lista funktionens studerade egenskaper. Eleverna listar egenskaperna hos en funktion i enlighet med forskningsdesignen. Läraren, till höger om grafen för funktionen, skriver ner de namngivna egenskaperna med en markör på den interaktiva tavlan.

Ris. 1

Funktionsegenskaper:

3. Att sätta upp mål för eleverna.

I slutet av studien rapporterar läraren att de idag i lektionen kommer att bekanta sig med en annan egenskap hos en funktion - reversibilitet. För att på ett meningsfullt sätt studera nytt material uppmanar läraren barnen att bekanta sig med de viktigaste frågorna som eleverna måste svara på i slutet av lektionen. Frågor i formuläret åhörarkopior Varje elev har en (delas ut före lektionen).

Frågor:

1. Vilken funktion kallas invertibel?

2. Vilken funktion kallas inversen?

3. Hur är definitionsdomänerna och värdeuppsättningarna för direkta och omvända funktioner relaterade till varandra?

4. Formulera ett tillräckligt villkor för en funktions inverterbarhet.

5. Minskar eller ökar motsatsen till en ökande funktion?

6. Är inversen av en udda funktion jämn eller udda?

7. Hur är graferna för ömsesidigt inversa funktioner placerade?

4. Presentation av nytt material.

1) Konceptet med en inverterbar funktion. Tillräckligt skick för reversibilitet.

På den interaktiva tavlan jämför läraren graferna för två funktioner vars definitionsdomäner och värdeuppsättningar är desamma, men en av funktionerna är monoton och den andra inte (fig. 2). Funktionen har alltså en egenskap som inte är karakteristisk för funktionen: vilket nummer som helst från uppsättningen funktionsvärdenf ( x ) oavsett vad är det värdet av en funktion vid endast en punkt, därigenom leder läraren eleverna till begreppet en inverterbar funktion.

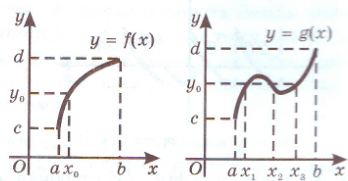
Ris. 2

Läraren formulerar sedan definitionen av en inverterbar funktion och genomför ett bevis på den inverterbara funktionssatsen med hjälp av grafen för en monoton funktion på den interaktiva skrivtavlan.

Definition 1. Funktionen kallasreversibel , om den tar något av dess värden endast vid en punkt i uppsättningenX .

Sats. Om funktionen är monoton på apparatenX , då är den reversibel.

Bevis:

Låt funktionen y=f(x) ökar på uppsättningenX släpp det X 1 ≠x 2 – två punkter i setetX .

För att vara specifik, låtX 1 < X 2 . Sedan från det faktum attX 1 < X 2 på grund av ökningen av funktionen följer det attf(x 1 ) < f(x 2 ) .

Således motsvarar olika värden av argumentet olika betydelser funktioner, dvs. funktionen är inverterbar.

Satsen bevisas på liknande sätt i fallet med en minskande funktion.

(När beviset på teoremet fortskrider använder läraren en markör för att göra alla nödvändiga förklaringar på ritningen)

Innan han formulerar definitionen av en invers funktion ber läraren eleverna att bestämma vilken av de föreslagna funktionerna som är inverterbar? Den interaktiva whiteboardtavlan visar funktionsdiagram (fig. 3, 4) och skriver flera analytiskt definierade funktioner:

A ) b )

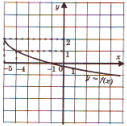
Ris. 3 Fig. 4

V ) y = 2x + 5; G ) y = - + 7.

Kommentar. Funktionens monotoni ärtillräcklig villkor för existensen av den inversa funktionen. Men detär inte ett nödvändigt villkor.

Läraren ger exempel på olika situationer när en funktion inte är monoton utan reversibel, när en funktion inte är monoton och inte reversibel, när den är monoton och reversibel.

2) Begreppet en invers funktion. Algoritm för att komponera en invers funktion.

Definition 2. Låt den inverterbara fungeray=f(x) definieras på setetX och dess värdeområdeE(f)=Y . Låt oss matcha var och eny från Y det är den enda meningenX, vid vilken f(x)=y. Då får vi en funktion som är definierad påY, A X – område av funktionsvärden. Denna funktion är betecknadx=f -1 (y), och ring omvänd i förhållande till funktiony=f(x), .

Sedan introducerar läraren eleverna för en metod för att hitta en invers funktion given analytiskt.

Algoritm för att komponera en invers funktion för en funktion y = f ( x ), .

Kontrollera funktioneny=f(x) reversibel på intervalletX .

ExpressvariabelX genom på från Eq. y=f(x), med hänsyn till det.

I den resulterande jämlikheten, byt platsX Och på. Istället för x=f -1 (y) skriva y=f -1 (x).

Med hjälp av specifika exempel visar läraren hur man använder denna algoritm.

Exempel 1. Visa det för en funktiony=2x-5

Lösning . Linjär funktion y=2x-5 bestäms på R, ökar med R och dess värdeområde ärR. Detta betyder att den omvända funktionen existerar påR . För att hitta dess analytiska uttryck löser vi ekvationeny=2x-5 relativt X ; vi får det. Låt oss omdesigna variablerna och få den önskade inversa funktionen. Den definieras och ökar på R.

Exempel 2. Visa det för en funktiony=x 2 , x ≤ 0 det finns en omvänd funktion, och hitta dess analytiska uttryck.

Lösning . Funktionen är kontinuerlig, monoton i sin definitionsdomän, därför är den inverterbar. Efter att ha analyserat funktionens definitionsdomäner och värdeuppsättningar görs en motsvarande slutsats om det analytiska uttrycket för den omvända funktionen, som har formen.

3) Egenskaper för ömsesidigt omvända funktioner.

Fastighet 1. Om g – funktion invers till f , då f – funktion invers till g (funktionerna är ömsesidigt inversa), medanD ( g )= E ( f ), E ( g )= D ( f ) .

Fastighet 2. Om en funktion ökar (minskar) på mängden X, och Y är funktionens värdeintervall, så ökar (minskar) den omvända funktionen på Y.

Fastighet 3. För att få grafen för en funktion som är invers till en funktion måste du transformera grafen för funktionen symmetriskt med avseende på den räta linjeny=x .

Fastighet 4. Om en udda funktion är inverterbar är dess invers också udda.

Fastighet 5. Om funktionerna f ( x ) Och ömsesidigt omvänt, då är det sant för vem som helst, och det är sant för alla.

Exempel 3. Rita en graf över den inversa funktionen, om möjligt.

Lösning. Genom hela sin definitionsdomän denna funktion har ingen invers eftersom den inte är monoton. Låt oss därför betrakta intervallet över vilket funktionen är monoton: det betyder att det omvända existerar. Vi hittarhenne . För att göra detta, uttrycker vix genomy : . Låt oss omdesigna det till den inversa funktionen. Låt oss plotta funktionerna (fig. 5) och se till att de är symmetriska med avseende på den räta linjeny = x .

Ris. 5

Exempel 4. Hitta uppsättningen värden för var och en av de ömsesidiga funktionerna om det är känt att.

Lösning. Enligt egenskap 1 av ömsesidigt omvända funktioner har vi.

5 . Sammanfattande

Utföra diagnostiskt arbete. Syftet med detta arbete är att bestämma graden av assimilering utbildningsmaterial diskuteras i föreläsningen. Studenterna ombeds svara på frågorna som ställdes i början av föreläsningen.

6 . Iscensättning läxa.

1. Förstå föreläsningsmaterialet, lära sig grundläggande definitioner och påståenden av satser.

2. Bevisa egenskaperna hos ömsesidigt omvända funktioner.

Lektion 2. Workshop om ämnet ”Definition av en invers funktion. Tillräckligt villkor för en funktions inverterbarhet"

Mål: att utveckla förmågan att tillämpa teoretisk kunskap om ämnet vid problemlösning, att överväga huvudtyperna av problem för att studera en funktion för reversibilitet, för att konstruera en invers funktion.

Workshop lektionsplan:

1. Organisatoriskt ögonblick.

2. Uppdatering av kunskaper (framarbete av studenter).

3. Konsolidering av det studerade materialet (lösa problem).

4. Sammanfattning av lektionen.

5. Göra läxor.

Under lektionerna.

1. Att organisera tid.

Hälsar på läraren, kontrollerar elevernas beredskap för lektionen.

2. Uppdaterar kunskap. ( studenters frontarbete).

Eleverna ombeds utföra följande uppgifter muntligen:

1. Formulera ett tillräckligt villkor för en funktions inverterbarhet.

2. Bland de funktioner vars grafer visas i figuren, ange de som är reversibla.

3. Formulera en algoritm för att komponera en funktion invers till en given.

4. Finns det datainversa funktioner? Om svaret är ja, hitta dem:

A) ; b ) ; c ) .

5. Är de funktioner vars grafer visas i figuren inversa (fig. 6)? Motivera ditt svar.

Ris. 6

3. Konsolidering av lärt material (problemlösning).

Konsolidering av det studerade materialet består av två steg:

Enskild självständigt arbete studenter;

Sammanfattning av resultatet av individuellt arbete.

I första skedet erbjuds eleverna kort med uppgifter som de genomför självständigt.

Övning 1.

Är funktioner inverterbara över hela sin domän? Om ja, hitta det omvända till det.

a) ; b) ; c) .

Uppgift 2.

Är funktionerna inversa?

A);

b ) .

Uppgift 3.

Betrakta funktionen på vart och ett av de angivna intervallen; om funktionen är inverterbar på detta intervall, definiera sedan dess invers analytiskt, ange definitionsdomänen och värdeintervall:

a ) R ; b ) ; d ) [-2;0].

Uppgift 4.

Bevisa att funktionen är oåterkallelig. Hitta den inversa funktionen på intervallet och rita dess graf.

Uppgift 5.

Rita grafen av funktionen och avgör om det finns en invers funktion för den. Om ja, rita sedan den inversa funktionen i samma ritning och definiera den analytiskt:

a ) ; b ) .

I stadiet för att summera resultaten av elevernas individuella arbete kontrolleras uppgifter endast med registrering av mellanresultat. De problem som orsakade de största svårigheterna övervägs på tavlan, antingen avslöjar sökandet efter lösningar eller registrerar hela lösningen.

4. Sammanfattning av lektionen (reflektion).

Eleverna erbjuds ett mini-enkät:

Vad tyckte jag om lektionen?______________________________

Vad gillade jag inte med lektionen?______________________________

_________________________________________________________________

Ange det påstående som passar dig bäst:

1) Jag kan självständigt undersöka en funktion för reversibilitet, konstruera dess invers och är säker på att resultatet är korrekt.

2) Jag kan undersöka en funktion för invertibilitet, konstruera dess invers, men jag är inte alltid säker på att resultatet är korrekt, jag behöver hjälp av mina vänner.

3) Jag kan praktiskt taget inte studera funktionen för reversibilitet, konstruera det omvända, jag behöver ytterligare råd från läraren.

Var kan jag tillämpa de förvärvade kunskaperna?____________________ _________________________________________________________________

5. Göra läxor.

№ 10,3, 10,6 (c, d), 10,7 (c, d), 10,9 (c, d), 10,13 (c, d), 10,18.(Mordkovich, A.G. Algebra och början av matematisk analys 10:e klass. Klockan 14.00, del 2. Problembok för studenter läroanstalter (profilnivå) / A.G. Mordkovich, P.V. Semenov. - M.: Mnemosyne, 2014. - 384 s.)

I. Kommunicera ämnet och syftet med lektionen

II. Upprepning och konsolidering av det täckta materialet

1. Svar på frågor om läxor (analys av olösta problem).

2. Övervakning av assimileringen av materialet (självständigt arbete).

Alternativ 1

Alternativ 2

Undersök funktionen och rita den:

III. Att lära sig nytt material

Med hjälp av funktionens analytiska form är det lätt att hitta motsvarande värde för funktionen y för valfritt värde i argumentet. Det omvända problemet uppstår ofta: värdet på y är känt och det är nödvändigt att hitta värdet på argumentet x , där det uppnås.

Exempel 1

Låt oss hitta värdet på argumentet x om värdet på funktionenär lika med: a) 2; b) 7/6; i 1.

Från funktionens analytiska formuttryck variabeln x och få: 4 xy - 2y = 3 x + 1 eller x(4y - 3) = 2y + 1, varifrån. Nu är det enkelt att lösa problemet:

Fungera kallas inversen av funktionen. Eftersom det är vanligt att beteckna en funktions argument med bokstaven x, och värdet av funktionen med bokstaven y, skrivs den inversa funktionen i formen

Vi kommer att ge de begrepp som behövs för att studera ämnet.

Definition 1. Funktion y = f(x), x ∈ X kallas invertibel om den tar något av dess värden endast vid en punkt x i mängden X (med andra ord, om olika värden på argumentet motsvarar olika värden på funktionen). Annars kallas funktionen irreversibel.

Exempel 2

Fungera Var och en av dess värden tar bara en punkt x och är reversibel (graf a). Fungerahar värden på y (till exempel y = 2) som uppnås vid två olika punkter x , och är irreversibel (graf b).

Följande sats är användbar när man överväger ämnet.

Sats 1. Om funktionen y = f (x), x ∈ X är monotont på mängden X, sedan är det inverterbart.

Exempel 3

Låt oss gå tillbaka till föregående exempel. Fungeraminskar (monotonisk) och är inverterbar över hela definitionsdomänen. Fungeraicke-monotona och irreversibla. Denna funktion ökar dock med intervallen (-∞; -1] och . Därför är funktionen inverterbar på sådana intervall. Till exempel är funktionen inverterbar på intervallet x ∈ [-1; 1].

Definition 2. Låt y = f (x), x ∈ X är en inverterbar funktion och E(f) = Y . Låt oss matcha var och en Y är det enda värdet på x för vilket f(x ) = y (dvs den enda roten i ekvationen f(x ) = y relativt variabeln x). Då får vi en funktion som är definierad på setet Y (mängden X är dess värdeområde). Denna funktion betecknas med x – f -1 (y), y ∈ Y och kallas inversen av funktionen y = f (x), x ∈ X. Figuren visar funktionen y = f (x) och invers funktion x = f-1 (y).

Framåt- och inversfunktionerna har samma monotoni.

Sats 2. Om funktionen y = f (x) ökar (minskar) på mängden X, och Y är dess värdeområde, sedan den inversa funktionen x = f -1 (y ) ökar (minskar) på uppsättningen Y.

Exempel 4

Fungera minskar på setetoch har många betydelserOmvänd funktionminskar också på setetoch har många betydelserDet är uppenbart att graferna för funktioner Och sammanfaller, eftersom dessa funktioner leder till samma samband mellan variablerna x och y: 4xy - 3x - 2y - 1 = 0.

Det är brukligt för oss att argumentet för en funktion betecknas med bokstaven x och värdet på funktionen med bokstaven y. Därför kommer vi att skriva den inversa funktionen i formen y = f-1 (x) (se exempel 1).

Sats 3. Grafer för funktionen y = f (x) och den inversa funktionen y = f -1 symmetrisk till den relativa räta linjen y = x.

Exempel 5

För funktionen y = 2x - 4 hittar vi den inversa funktionen: y + 4 = 2x, varav x = 1/2y + 2. Låt oss introducera ombeteckningar x↔ y och skriv den inversa funktionen i formen y = 1/2x + 2. Således, för funktionen f (x) = 2x – 4 omvänd funktion f -1(x ) = 1/2x + 2. Låt oss bygga grafer över dessa funktioner. Det kan ses att graferna är symmetriska till den relativa räta linjen y = x.

Funktion f -1 (x ) = 1/2x + 2 invers av funktionen f (x) = 2x - 4. Men också funktionen f (x) = 2x - 4 är inversen av funktionen f -1(x ) = 1/2x + 2. Därför fungerar funktionerna f(x) och f-1 (x) kallas mer korrekt reciprocal. I det här fallet är följande jämlikheter uppfyllda: f -1 (f (x)) = x och f (f -1 (x) = x.

IV. Kontrollfrågor

1. Reversibla och irreversibla funktioner.

2. Inverterbarhet av en monoton funktion.

3. Definition av den inversa funktionen.

4. Monotonicitet av direkta och inversa funktioner.

5. Grafer över direkta och inversa funktioner.

V. Lektionsuppgift

3 § nr 1 (a, b); 2 (c, d); 3 (a, d); 4 (c, d); 5 (a, c).

VI. Hemläxa

3 § nr 1 (c, d); 2 (a, b); 3 (b, c); 4 (a, b); 5 (b, d).

VII. Sammanfattning av lektionen

Lektionens mål:

Pedagogisk:

• bygga kunskap på nytt ämne i enlighet med programmaterialet;
• studera egenskapen för reversibilitet för en funktion och lära ut hur man hittar den inversa funktionen av en given funktion;

Utvecklandet:

• utveckla självkontrollförmåga, innehållsmässigt tal;
• behärska begreppet invers funktion och lära sig metoder för att hitta den inversa funktionen;

Pedagogiskt: att utveckla kommunikativ kompetens.

Utrustning: dator, projektor, duk, interaktiv skrivtavla SMART Board, utdelat material (självständigt arbete) för grupparbete.

Under lektionerna.

1. Organisatoriskt ögonblick.

Mål – förbereda eleverna för arbete i klassen:

Definition av frånvarande,

Få eleverna på humör för arbete, organisera uppmärksamhet;

Ange ämnet och syftet med lektionen.

2. Uppdatera elevernas grundläggande kunskaper. Frontalundersökning.

Mål - fastställa korrektheten och medvetenheten om det studerade teoretiska materialet, upprepning av det behandlade materialet.<Приложение 1 >

En graf över en funktion visas på den interaktiva skrivtavlan för eleverna. Läraren formulerar en uppgift - överväg grafen för en funktion och lista funktionens studerade egenskaper. Eleverna listar egenskaperna hos en funktion i enlighet med forskningsdesignen. Läraren, till höger om grafen för funktionen, skriver ner de namngivna egenskaperna med en markör på den interaktiva tavlan.

Funktionsegenskaper:

I slutet av studien rapporterar läraren att de idag i lektionen kommer att bekanta sig med en annan egenskap hos en funktion - reversibilitet. För att på ett meningsfullt sätt studera nytt material uppmanar läraren barnen att bekanta sig med de viktigaste frågorna som eleverna måste svara på i slutet av lektionen. Frågorna skrivs på en vanlig tavla och varje elev har dem som åhörarkopior (delas ut innan lektionen)

1. Vilken funktion kallas invertibel?
2. Är någon funktion inverterbar?
3. Vilken funktion kallas inversen av ett datum?
4. Hur är definitionsdomänen och uppsättningen värden för en funktion och dess omvända relaterade?
5. Om en funktion ges analytiskt, hur kan man definiera den inversa funktionen med en formel?
6. Om en funktion ges grafiskt, hur ritar man dess inversa funktion?

3. Förklaring av nytt material.

Mål - generera kunskap om ett nytt ämne i enlighet med programmaterialet; studera egenskapen för reversibilitet för en funktion och lära ut hur man hittar den inversa funktionen av en given funktion; utveckla innehållsmässigt tal.

Läraren presenterar materialet i enlighet med materialet i stycket. På den interaktiva skrivtavlan jämför läraren graferna för två funktioner vars definitionsdomäner och värdeuppsättningar är desamma, men en av funktionerna är monoton och den andra inte, vilket introducerar eleverna till konceptet med en inverterbar funktion .

Läraren formulerar sedan definitionen av en inverterbar funktion och genomför ett bevis på den inverterbara funktionssatsen med hjälp av grafen för en monoton funktion på den interaktiva skrivtavlan.

Definition 1: Funktionen y=f(x), x X anropas reversibel, om den tar något av dess värden endast vid en punkt av uppsättningen X.

Sats: Om en funktion y=f(x) är monoton på en mängd X, så är den inverterbar.

Bevis:

1. Låt funktionen y=f(x)ökar med X släpp det x 1 ≠x 2- två poäng i setet X.
2. För att vara specifik, låt x 1< x 2.
   Sedan från det faktum att x 1< x 2 följer det f(x 1) < f(x 2).
3. Således motsvarar olika värden på argumentet olika värden på funktionen, dvs. funktionen är inverterbar.

(När beviset på teoremet fortskrider använder läraren en markör för att göra alla nödvändiga förklaringar på ritningen)

Innan han formulerar definitionen av en invers funktion ber läraren eleverna att bestämma vilken av de föreslagna funktionerna som är inverterbar? Den interaktiva skrivtavlan visar grafer över funktioner och skriver flera analytiskt definierade funktioner:

B)

G) y = 2x + 5

D) y = -x 2 + 7

Läraren introducerar definitionen av en invers funktion.

Definition 2: Låt den inverterbara fungera y=f(x) definieras på setet X Och E(f)=Y. Låt oss matcha var och en y från Y det är den enda meningen X, vid vilken f(x)=y. Då får vi en funktion som är definierad på Y, A X– funktionsområde

Denna funktion är betecknad x=f -1 (y) och kallas inversen av funktionen y=f(x).

Eleverna uppmanas att dra en slutsats om sambandet mellan definitionsdomänen och uppsättningen av värden för inversa funktioner.

För att överväga frågan om hur man hittar inversen av en given funktion lockade läraren två elever. Dagen innan fick barnen ett uppdrag av läraren att självständigt analysera de analytiska och grafiska metoderna för att hitta den omvända funktionen av en given funktion. Läraren fungerade som konsult för att förbereda eleverna för lektionen.

Meddelande från den första studenten.

Obs: funktionens monotoni är tillräcklig villkor för existensen av den inversa funktionen. Men det är inte ett nödvändigt villkor.

Eleven gav exempel på olika situationer när en funktion inte är monoton utan inverterbar, när en funktion inte är monoton och inte inverterbar, när den är monoton och inverterbar

Eleven introducerar sedan eleverna för en metod för att hitta den inversa funktionen som ges analytiskt.

Hitta algoritm

1. Se till att funktionen är monoton.
2. Uttryck variabeln x i termer av y.
3. Byt namn på variabler. Istället för x=f -1 (y) skriv y=f -1 (x)

Sedan löser han två exempel för att hitta den inversa funktionen av ett givet.

Exempel 1: Visa att det för funktionen y=5x-3 finns en invers funktion och hitta dess analytiska uttryck.

Lösning. Den linjära funktionen y=5x-3 definieras på R, ökar på R, och dess värdeområde är R. Detta betyder att den inversa funktionen finns på R. För att hitta dess analytiska uttryck, lös ekvationen y=5x- 3 för x; vi får Detta är den nödvändiga inversa funktionen. Den definieras och ökar på R.

Exempel 2: Visa att det för funktionen y=x 2, x≤0 finns en invers funktion, och hitta dess analytiska uttryck.

Funktionen är kontinuerlig, monoton i sin definitionsdomän, därför är den inverterbar. Efter att ha analyserat funktionens definitionsdomäner och värdeuppsättningar görs en motsvarande slutsats om det analytiska uttrycket för den inversa funktionen.

Den andra eleven gör en presentation om grafisk metod för att hitta den inversa funktionen. Under sin förklaring använder eleven funktionerna hos den interaktiva skrivtavlan.

För att få en graf av funktionen y=f -1 (x), invers till funktionen y=f(x), är det nödvändigt att transformera grafen för funktionen y=f(x) symmetriskt med avseende på den räta linjen y=x.

Under förklaringen på den interaktiva skrivtavlan utförs följande uppgift:

Konstruera en graf för en funktion och en graf för dess inversa funktion i samma koordinatsystem. Skriv ner det analytiska uttrycket för den inversa funktionen.

4. Primär konsolidering av nytt material.

Mål - fastställa riktigheten och medvetenheten om förståelsen av det studerade materialet, identifiera luckor i den primära förståelsen av materialet och korrigera dem.

Eleverna delas in i par. De får arbetsblad, där de utför arbetet i par. Tiden för att slutföra arbetet är begränsad (5-7 minuter). Ett par elever arbetar vid datorn, projektorn stängs av under denna tid och resten av barnen kan inte se hur eleverna arbetar på datorn.

I slutet av tiden (det antas att majoriteten av eleverna har slutfört arbetet) visas elevernas arbete på den interaktiva tavlan (projektorn slås på igen), där det under kontrollen avgörs om uppgiften genomfördes korrekt i par. Vid behov utför läraren korrigerande och förklarande arbete.

Självständigt arbete i par<Bilaga 2 >

5. Lektionssammanfattning. Angående frågorna som ställdes inför föreläsningen. Tillkännagivande av betyg på lektionen.

Läxor §10. Nr. 10.6(a,c) 10.8-10.9(b) 10.12 (b)

Algebra och början av analys. Betyg 10 I 2 delar för allmänna utbildningsinstitutioner (profilnivå) / A.G. Mordkovich, L.O. Denishcheva, T.A. Koreshkova, etc.; redigerad av A.G. Mordkovich, M: Mnemosyne, 2007

Omvänd funktion

Lektionstext

• Anteckningar lektion 1-3 (Morozova I.A.)

  Namn på ämnet Algebra och början av matematisk analys Klass 10 UMK Algebra och början av matematisk analys. 10-11 årskurser. Klockan 2 Del 1. Lärobok för studenter vid allmänna läroanstalter ( en grundläggande nivå av)/ A.G. Mordkovich. – 10:e uppl., raderad. – M.: Mnemosyne, 2012. Del 2. Problembok för studenter vid allmänna läroanstalter (grundläggande nivå) / [A.G. Mordkovich et al; redigerad av A.G. Mordkovich. – 10:e uppl., raderad. – M.: Mnemosyne, 2012. Grundläggande inlärningsnivå Lektionsämne: Invers funktion. (3 timmar) Lektion 1. Mål för lektionen: introducera begreppen reversibla och inversa funktioner; utföra ett bevis på satsen om monotoniteten hos direkta och inversa funktioner; identifiera och motivera geometrisk betydelse reversibilitet för en funktion Lektionens mål: - att utveckla förmågan att hitta den inversa funktionen för en given; - utveckla förmågan att bygga en graf över en invers funktion. Planerade resultat: Vet: definition av en reversibel funktion, invers funktion, tecken på reversibilitet för en funktion. Kunna: hitta formeln för en funktion invers till en given; bygga en graf av en invers funktion med hjälp av grafen för en given funktion. Teknisk support för lektionen: dator, skärm, projektor, lärobok. Lektionens framsteg I. Organisatoriskt ögonblick. II. Kontrollera läxor (analys av uppgifter som orsakade svårigheter för eleverna) III. Verifieringsarbete. Alternativ 1 1. Givet en funktion a) Undersök funktionen för monotoni om x > 2. b) Hitta de största och minsta värdena för funktionen på intervallet [–1,5; 1,5]. 2. Undersök funktionen där x > 0 för avgränsning. 3. Undersök funktionen för paritet. Alternativ 2 1. Given funktion a) Undersök funktionen för monotoni om x< 2. б) Найдите наибольшее и наименьшее значения функции на отрезке [–4,5; –3,1]. 2. Исследуйте функцию где х < 0, на ограниченность. 3. Исследуйте функцию на четность. Вариант 3 1. Дана функция а) Исследуйте функцию на монотонность, если х < –1. б) Найдите наибольшее и наименьшее значения функции на отрезке [–2; 0,4]. 2. Исследуйте функцию где х < –1, на ограниченность. 3. Исследуйте функцию на четность. Вариант 4 1. Дана функция а) Исследуйте функцию на монотонность, если х  1. б) Найдите наибольшее и наименьшее значения функции на отрезке . 2. Исследуйте функцию где х >2, för begränsningar. 3. Undersök funktionen för paritet. Lösa alternativ 1 och 3 i testarbetet. Alternativ 1 och 2 är något enklare än alternativ 3 och 4. Alternativ 1 1. Låt oss beteckna a) Låt sedan funktionen minska med (–; 2]. b) Eftersom funktionen minskar med (–∞; 2), så Svar: a) minskar; b) unaib. = 12,25; unaim. = 0,25. 2. där x > 0. Funktionen avgränsas ovanför av den räta linjen y = 0, vilket betyder att funktionen avgränsas ovanför av den räta linjen y = 1. Svar: avgränsas ovanför. 3. – symmetrisk om ursprunget. Det betyder att funktionen är udda. Svar: udda. Alternativ 3 1. a) Låt oss beteckna grafen som en parabel med dess vertex i punkten (–1; –1) och skär 0x-axeln i punkterna x = 0 och x = –2. Om x > –1 ökar funktionen. b) På segmentet [–2; 0.4] och Svar: a) ökar; b) unaib. = 0,96; unaim. = 0. 2. där x< –1. Функция ограничена снизу прямой у = 0, значит, функция ограничена снизу прямой у = 2. Ответ: ограничена снизу. 3. – симметрична относительно начала координат. Если х = 0, то Имеем: значит, функция ни четная, ни нечетная. Ответ: ни четная, ни нечетная. IV. Объяснение нового материала. 1. Для введения понятия обратимой функции можно использовать либо подвижные модели, либо изображение обратимых и необратимых функций на прозрачной пленке, перевернув которую можно показать, как область определения и область значения функции «меняются местами» и в каком случае обеспечивается однозначность обратной функции. 2. Для первичного закрепления материала учащиеся выполняют следующее задание. Среди функций, графики которых изображены на рисунке, укажите обратимые. 3. Теорема 1. Подчеркиваем учащимся, что в теореме сформулирован признак обратимости функции (достаточное условие). В то же время монотонность не является необходимым условием обратимости. Динамическая пауза. V. Формирование умений и навыков. Упражнения, решаемые на этом уроке, направлены на аналитическое задание функции, обратной данной. № 3.1 (а; б), № 3. 2 (а; б). При выполнении этих упражнений следует предупредить формализм в аналитическом задании функции путем простого преобразования уравнения. Учащиеся должны обосновать существование обратной функции. Решение: № 3.1 (б). Линейная функция у = 2 + 4х определена на R, возрастает на R(k  0), E(f) = R. Значит, на R существует обратная функция. – искомая обратная функция, возрастающая на R. Ответ: № 3.2 (б). Функция убывает на всей области определения, значит, существует обратная функция, определенная и убывающая на Ответ: V. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. Домашнее задание: № 3.1 (в; г) – № 3.2 (в; г). Урок 2. Цель урока: выявить и обосновать геометрический смысл обратимости функции Задачи урока: - развивать умение находить обратную функцию для заданной; - формировать умение строить график обратной функции. Планируемые результаты: Знать: определение обратимой функция, обратной функции, признак обратимости функции. Уметь: находить формулу функции, обратной данной; строить график обратной функции, используя график данной функции. Техническое обеспечение урока компьютер, экран, проектор, учебник. Ход урока I. Организационный момент. II. Проверка домашнего задания (разбор заданий, вызвавших затруднения учащихся) III. Работа в группах. Карточка 1. Карточка 2. IV. Объяснение нового материала. Устанавливая геометрический смысл обратимости функции, учащиеся формулируют способ построения графика обратной функции с помощью преобразования осевой симметрии. Графики функции у = f(х) и обратной функции у = f-1 симметричны относительной прямой у = х. Для функции у = 2х - 4 найдем обратную функцию: у + 4 = 2х, откуда х = 1/2у + 2. Введем переобозначения х ↔ у и запишем обратную функцию в виде у = 1/2х + 2. Таким образом, для функции f(х) = 2х – 4 обратная функция f-1(x) = 1/2х + 2. Построим графики этих функций. Видно, что графики симметричны относительной прямой у = х. Функция f-1(x) = 1/2х + 2 обратная по отношению к функции f(х) = 2х - 4. Но и функция f(х) = 2х - 4 является обратной по отношению к функции f-1(x) = 1/2х + 2. Поэтому функции f(х) и f-1(х) корректнее называть взаимообратными. При этом выполнены равенства: f-1(f(х)) = х и f(f-1(x) = x. Динамическая пауза. V. Формирование умений и навыков. Упражнения, решаемые на этом уроке, направлены на построение графика обратной функции с помощью осевой симметрии. № 3.3 (а; б), № 3. 4 (а; б), № 3.5* (а; б). Решение: № 3. 4 (б). Графиком является кубическая парабола, полученная из графика у = х3 сдвигом вправо по оси 0х на 2 единицы. Функция возрастает на R, значит, существует обратная функция, заданная и возрастающая на R. Ответ: V. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. – Каков характер монотонности прямой и обратной функций? – Как построить график обратной функции, используя график данной функции? Домашнее задание: № 3.3 (в; г) – № 3.4 (в; г) № 3.5 * (в; г) – по желанию. Урок 3. Цель урока: проверить степень усвоения теоретического материала и умения применять его при выполнении письменной работы Задачи урока: - развивать умение находить обратную функцию для заданной; - развивать умение строить график обратной функции. Планируемые результаты: Знать: определение обратимой функция, обратной функции, признак обратимости функции. Уметь: находить формулу функции, обратной данной; строить график обратной функции, используя график данной функции. Техническое обеспечение урока компьютер, экран, проектор, учебник. Ход урока I. Организационный момент. II. Проверка домашнего задания (разбор заданий, вызвавших затруднения учащихся) III. Зачетная работа Вариант 1. Вариант 2. Итоги урока. Вопросы учащимся: – Какая функция называется обратимой? – Сформулируйте признак обратимости функции. –Дайте определение обратной функции. – Каков характер монотонности прямой и обратной функций? – Как построить график обратной функции, используя график данной функции? Домашнее задание: §3, примеры 1-3.

  Ladda ner: Algebra 10kl - Notes lektion 1-3 (Morozova I. A.).docx

• Lektion 1 (Samoilova G.A.)

  Algebra och början av analys årskurs 10 UMC: Algebra och början på analys årskurs 10-11, A.G. Mordkovich, Moskva 2013 Inlärningsnivå: grundläggande Ämne: Invers funktion Totalt antal timmar: 3 timmar På ämne: lektion nr 1 Syfte med lektionen: Utbildning: Introducera och konsolidera definitionen av den inversa funktionen; studera egenskapen för reversibilitet för en funktion och lära ut hur man hittar den inversa funktionen av en given funktion; Utveckling: utveckla självkontrollförmåga, innehållsmässigt tal; behärska begreppet invers funktion och lära sig metoder för att hitta den inversa funktionen; Pedagogiskt: att utveckla kommunikativ kompetens. Lektionens mål: 1. Att introducera eleverna till inverterbara funktioner och deras grafer. 2. Berika elevernas erfarenhet av att tillägna sig ny kunskap baserad på befintlig teoretisk kunskap, samt genom att använda välbekanta praktiska situationer Planerade resultat: Efter att ha studerat detta ämne ska eleverna veta: Definition av en inverterbar funktion; plotta en reversibel funktion; exempel på funktioner från livet; tekniker för jämförelse, generalisering, förmåga att dra slutsatser; Efter att ha studerat detta ämne ska eleverna kunna: självständigt fylla på och systematisera sina kunskaper: - bygga grafer över reversibla funktioner: - kunna dra slutsatser. Lektion teknisk support: handledning"Algebra och början av analys. 10:e klass (grundnivå)” A.G. Mordkovich. Tabeller numeriska funktioner . Dator, projektor, duk. Ytterligare metodiskt och didaktiskt stöd till lektionen: Metodhandbok för lärare ”Lektionsplaner för läroboken Algebra och början av analys åk 10-11”, A.G. Mordkovich, Volgograd 2013 Internetresurser https:// 1september.ru Lektionens innehåll: 1. Organisatoriskt ögonblick 2. Kontroll av restkunskaper 3. Studie av nytt material 4. Konsolidering 5. Lektionssammanfattning 6. Ställa läxor Lektionens framsteg: 1. Organisatorisk punkt 2 Kontroll av restkunskap 1). Upprepning och konsolidering av det material som omfattas 1. Svar på frågor om läxor (analys av olösta problem). 2. Övervakning av assimileringen av materialet (självständigt arbete). Alternativ 1 Gör en studie av funktionen och bygg dess graf: 3. Studera nytt material Med hjälp av funktionens analytiska form är det lätt att hitta motsvarande värde för funktionen y för vilket värde som helst av argumentet. Ofta uppstår det omvända problemet: värdet på y är känt och det är nödvändigt att hitta värdet på argumentet x vid vilket det uppnås. Exempel 1 Låt oss hitta värdet på argumentet x om värdet på funktionen är lika med: a) 2; b) 7/6; c) 1. Från funktionens analytiska form uttrycker vi variabeln x och får: 4xy - 2y = 3x + 1 eller x(4y - 3) = 2y + 1, varifrån. Nu är det lätt att lösa problemet: En funktion kallas inversen av en funktion. Eftersom det är vanligt att beteckna argumentet för en funktion med bokstaven x och värdet av funktionen med bokstaven y, skrivs den omvända funktionen i formen. Låt oss ge de begrepp som är nödvändiga för att studera ämnet. Definition 1. En funktion y = f(x), x ∈ X kallas inverterbar om den tar något av dess värden endast vid en punkt x i mängden X (med andra ord, om olika värden på argumentet motsvarar till olika värden för funktionen). Annars kallas funktionen irreversibel. Exempel 2 Funktionen tar varje värde endast vid en punkt x och är reversibel (graf a). Funktionen har värden y (till exempel y = 2) som uppnås vid två olika punkter x, och är irreversibel (graf b). Följande sats är användbar när man överväger ämnet. Sats 1. Om funktionen y = f(x), ∈ är monoton på mängden X, så är den inverterbar. Exempel 3 Låt oss återgå till föregående exempel. Funktionen är avtagande (monotonisk) och inverterbar över hela definitionsdomänen. Funktionen är icke-monoton och irreversibel. Denna funktion ökar dock med intervallen (-∞; -1] och . Därför är funktionen på sådana intervall inverterbar. Till exempel är funktionen inverterbar på intervallet x [-1;1 ]. Definition 2. Låt y = f(x), x ∈ X är en inverterbar funktion och E(f) = Y. Låt oss tilldela varje Y det unika värdet av x för vilket f(x) = y (dvs. d.v.s. den enda roten av ekvationen f(x) = y med avseende på variabeln x). Då får vi en funktion som är definierad på mängden Y (mängden X är dess värdeområde). Denna funktion betecknas x – f-1(y), y ∈ Y och kallas inversen av funktionen y = f(x), x ∈ X. Figuren visar funktionen y = f(x) och den inversa funktionen x = f-1(y). Framåt- och inversfunktionerna har samma monotoni. Sats 2. Om funktionen y = f(x) ökar (minskar) på mängden X, och Y är dess värdeområde, så ökar (minskar) den inversa funktionen x = f-1(y) på mängden Y. Exempel 4 Funktionen minskar på mängden och har många värden. Den inversa funktionen minskar också på mängden och har många värden. Uppenbarligen sammanfaller graferna för funktionerna och sammanfaller, eftersom dessa funktioner leder till samma förhållande mellan variablerna x och y: 4xy - 3x - 2y - 1 = 0. Det är vanligt för oss att argumentet för en funktion betecknas med bokstaven x och värdet på funktionen med bokstaven y. Därför kommer vi att skriva den inversa funktionen i formen y = f-1(x) (se exempel 1). Sats 3. Graferna för funktionen y = f(x) och den inversa funktionen y = f-1 är symmetriska till den relativa räta linjen y = x. Exempel 5 För funktionen y = 2x - 4 hittar vi den inversa funktionen: y + 4 = 2x, varav x = 1/2y + 2. Låt oss införa ombeteckningar x ↔ y och skriva den inversa funktionen på formen y = 1/2x + 2. Således, för funktionen f(x) = 2x – 4, är den inversa funktionen f-1(x) = 1/2x + 2. Låt oss bygga grafer för dessa funktioner. Det kan ses att graferna är symmetriska till den relativa räta linjen y = x. Funktionen f-1(x) = 1/2x + 2 är inversen av funktionen f(x) = 2x - 4. Men funktionen f(x) = 2x - 4 är också inversen av funktionen f-1 (x) = 1/2x + 2. Därför är det mer korrekt att kalla funktionerna f(x) och f-1(x) reciproka. I detta fall är likheterna uppfyllda: f-1(f(x)) = x och f(f-1(x) = x. 4. Förstärkning 1) Testfrågor: 1. Inverterbara och irreversibla funktioner. 2. Inverterbarhet av en monoton funktion. 3. Definition av den inversa funktionen. 4. Monotonicitet av direkta och inversa funktioner. 5. Grafer över direkta och inversa funktioner. 2) Lektionsuppgift § 3, nr 1 (a, b); 2 (c, d); 3 (a, d); 4 (c, d); 5 (a, c). 5. Lektionssammanfattning Vad lärde du dig för nytt i klassen idag? Vilka svårigheter stötte du på? Dra en slutsats om förhållandet mellan definitionsdomänen och uppsättningen värden för inversa funktioner. 4. Att sätta hemläxa § 3, nr 1 (c, d); 2 (a, b); 3 (b, c); 4 (a, b); 5 (b, d).

  Ladda ner: Algebra 10kl - lektion 1 (Samoilova G. A.).doc

• lektion 2 (Samoilova G.A.)

  Algebra och början av analys årskurs 10 UMC: Algebra och början på analys årskurs 10-11, A.G. Mordkovich, Moskva 2013 Inlärningsnivå: grundläggande Ämne: Invers funktion Totalt antal timmar: 3 Ämne: lektion nr 2 Syfte med lektionen: Utbildning: konsolidera definitionen av den inversa funktionen; konsolidera kunskap om reversibilitetsegenskaperna för en funktion och lära ut hur man hittar den inversa funktionen av en given funktion; Utveckling: utveckla självkontrollförmåga, innehållsmässigt tal; egna metoder för att hitta den inversa funktionen; Utbildning: att utveckla kommunikativ kompetens; Organisera problemsökningsarbete för eleverna Mål för lektionen: 1. Introducera eleverna för inverterbara funktioner och deras grafer. 2. Berika elevernas erfarenhet av att tillägna sig ny kunskap baserad på befintlig teoretisk kunskap, samt genom att använda välbekanta praktiska situationer Planerade resultat: Efter att ha studerat detta ämne ska eleverna veta: Definition av en inverterbar funktion; plotta en reversibel funktion; exempel på funktioner från livet; tekniker för jämförelse, generalisering. Efter att ha studerat detta ämne ska eleverna kunna: - självständigt fylla på och systematisera sina kunskaper: - bygga grafer över reversibla funktioner: - kunna dra slutsatser. Tekniskt stöd för lektionen: lärobok ”Algebra och analysens början. 10:e klass (grundnivå)” A.G. Mordkovich. Numeriska funktionstabeller. Dator, projektor, duk. Ytterligare metodiskt och didaktiskt stöd till lektionen: Metodhandbok för lärare ”Lektionsplaner för läroboken Algebra och början av analys åk 10-11”, A.G. Mordkovich, Volgograd 2013 Internetresurser https:// 1september.ru Lektionens innehåll: 1. Organisationsmoment 2. Kontrollera läxor 3. Konsolidering av det studerade materialet 4. Testarbete 5. Lektionssammanfattning 6. Ställa läxor 1. Organisatoriskt ögonblick. Läraren berättar för eleverna ämnet, syftet med lektionen och medlen för att uppnå det. 2. Kontrollera läxor 1) Problem som orsakar svårigheter löses vid tavlan 2) Frontalöversikt av den teoretiska delen av ämnet Frågor: 1. Vilken funktion kallas reversibel? 2. Är någon funktion inverterbar? 3. Vilken funktion kallas inversen av en given funktion? 4. Hur är definitionsdomänen och värdeuppsättningen för en funktion och dess omvända funktion relaterade? 5. Om en funktion ges analytiskt, hur kan man definiera den inversa funktionen med en formel? 6. Om en funktion ges grafiskt, hur ritar man dess inversa funktion? 3. Konsolidering av det studerade materialet 1) Arbeta med den färdiga ritningen (upprepning av egenskaperna hos en numerisk funktion). En graf över en funktion visas på den interaktiva skrivtavlan för eleverna. Läraren formulerar en uppgift - överväg grafen för en funktion och lista funktionens studerade egenskaper. Eleverna listar egenskaperna hos en funktion i enlighet med forskningsdesignen. Eleven, till höger om grafen för funktionen, skriver ner de namngivna egenskaperna med en markör på den interaktiva tavlan. Funktionens egenskaper: 1. D(f) = [-4;], E(y) = både på och på [-1;0] 6. ynaib- finns inte ynaim=0 vid x=0 7. xmax = -1 ,ymax = 2 xmin = -2, ymin = 1 xmin = 0, ymin = 0 8. Konvex nedåt på , konvex uppåt på . 2) Betrakta funktionen och hitta dess invers. (Arbeta vid tavlan, designa i en anteckningsbok). Given funktion y=x2,x∈)